Предмет: Математика,
автор: hoper123
Вычислить площадь фигуры, ограниченной параболой у=ах2+bх+с и прямой у=kх+b. Сделать чертеж
Приложения:
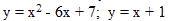
Ответы
Автор ответа:
1
Ответ:
============================================
Пошаговое объяснение:
Приложения:

Автор ответа:
1
Ответ:
20 5\6
Пошаговое объяснение:
1)у=х²-6х+7 , парабола ,
координаты вершины х₀=-в/2а, х₀=6/2=3 , у₀=9-18+7=-2, (3;-2) ,
доп точки у(0)=7, у(1)=3 ; у(6)=7
2)у=х+1 ,прямая , у(1)=2, у(6)7
3)Пределы интегрирования от 1 до 6 ,
S=∫(х+1- (х²-6х+7 ))dx=∫(- х²+7х-6 ) =(-x³/3+7х²\2-6х) | =
=(-x³/3+7х²\2-6х) | =(-6³/3+7*6²\2-6*6) - (-1³/3+7*1²\2-6*1)=
=(-216\3+252\2-36)-(-1\3+7\2-6)=
=-215\3+245\2-30=125\6=20 5\6
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kenzhebay
Предмет: Русский язык,
автор: alexnikiforoff
Предмет: Русский язык,
автор: daniyar02
Предмет: Геометрия,
автор: tsvetochnayapo
Предмет: Математика,
автор: jghjghjhg