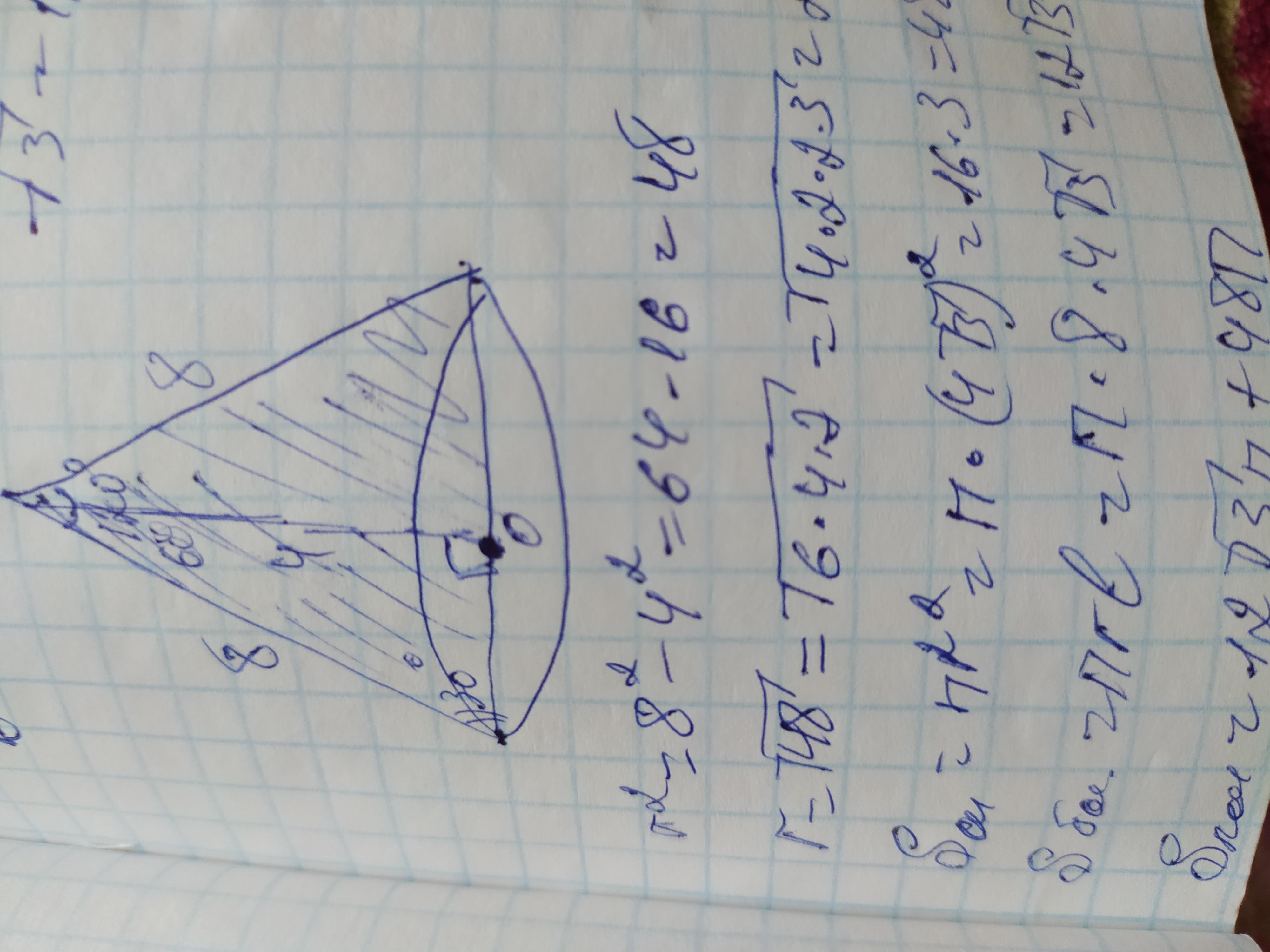
Осевое сечение конуса – треугольник со стороной 8см и прилежащим углом 120° . Найти площадь полной поверхности конуса.
Ответы
Ответ: Sпол=102,4π(см²)
Объяснение: проведём высоту h. Она делит основание осевого сечения пополам в точке О, на 2 радиуса, а также угол при вершине конуса пополам. Высота, радиус и образующая конуса составляют прямоугольный треугольник в котором радиус и высота являются катетами а образующая гипотенузой. В полученном треугольнике угол при вершине составляет 120/2=60°. В прямоугольном треугольнике сумма острых углов составляет 90°, поэтому угол между образующей и радиусом будет: 90-60=30°. Катет лежащий напротив него равен половине гипотенузы, поэтому высота h=8/2=4см. Найдём радиус r по теореме Пифагора:
r²=обр²-h²=8²-4²=64-16=48; r=√48см.
Sосн=πr²=π×(√48)²=48π(см²)
Sбок.пов=πrL, где L- образующая:
Sбок=π×√48×8=8π×4√3=32√3π(см²)
Sпол=Sбок+Sосн=
=32√3π+48π=32×1,7π+48π=54,4π+48π=
=102,4π(см²)