Предмет: Геометрия,
автор: kamusya200626
Помогите разобраться!
Приложения:
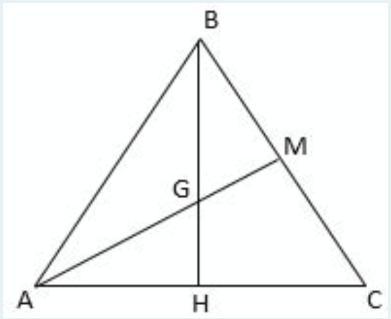

Ответы
Автор ответа:
1
Ответ:
8
Объяснение:
Найдем где
-- периметр. Так как центр тяжести является точкой пересечения медиан, то
-- медиана (так как проходит через
центр тяжести). А значит
Так как треугольник равнобедренный, то высота и медиана, проведенная к основанию совпадает, значит
-- высота, значит
-- прямоугольный. Тогда по теореме пифагора:
Пусть . Так как центр тяжести делит медианы в отношении 2:1 считая от вершины, то
.
Значит
Значит
(до этого уже нашли) и
.
То есть
.
Но как мы отметили выше,
Похожие вопросы
Предмет: Русский язык,
автор: Vova2894721
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: nosovatanechka
Предмет: Физика,
автор: Temabeg
Предмет: Математика,
автор: lolka572846