Предмет: Алгебра,
автор: vityamath
Упростите сложный радикал: 
Ответы
Автор ответа:
3
Решение приложено
=========================================================
Приложения:
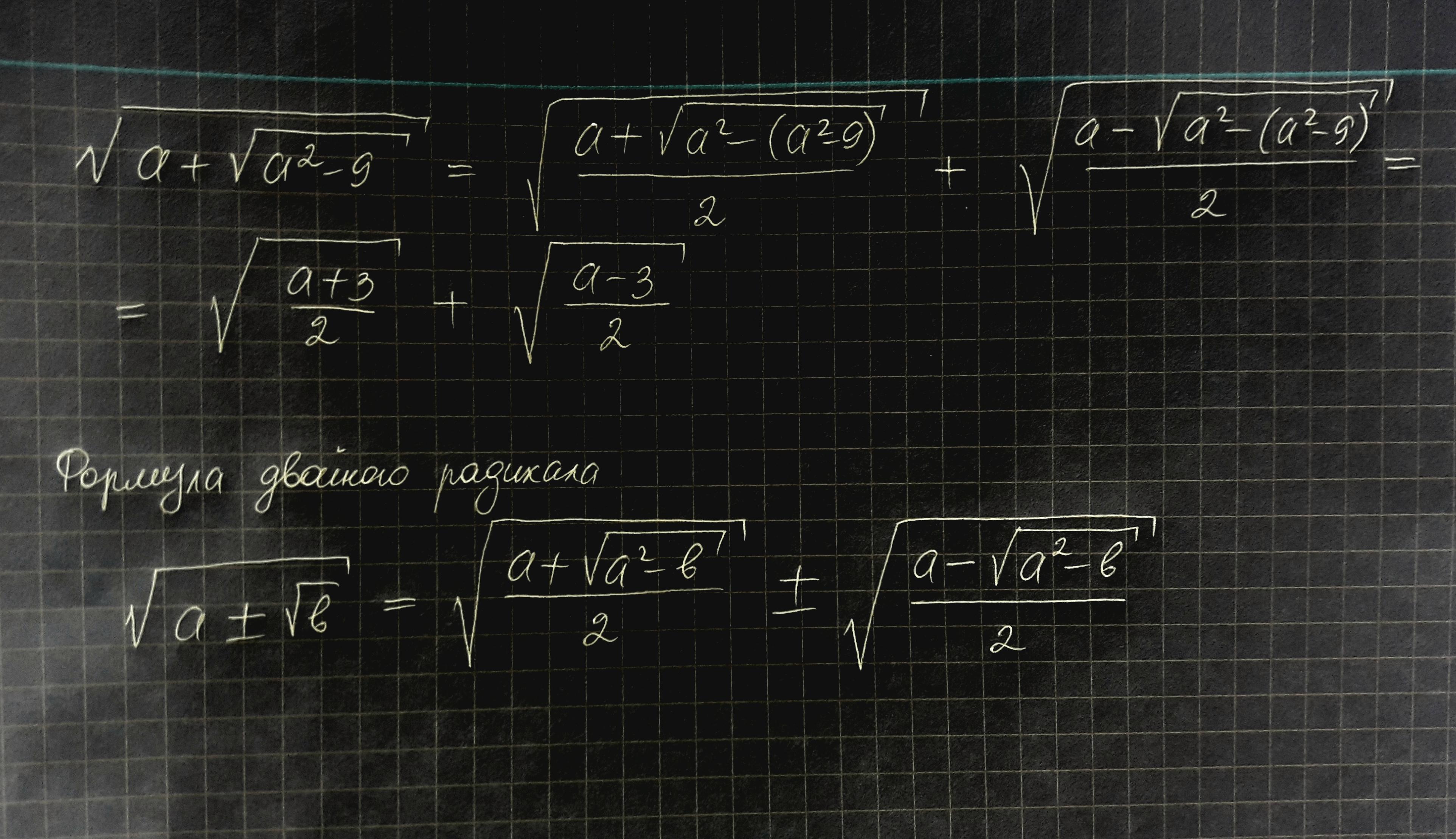
Аноним:
молодец!
круто!
Автор ответа:
1
Ответ:
Объяснение:
чтобы упростить выражение с квадратным корнем, нужно, чтобы подкоренное выражение было полным квадратом.
То есть под корнем должно быть (m+n)²
Так как (m+n)²=m²+2mn+n², значит в нашем случае
Первое что приходит в голову - это рассмотреть полный квадрат следующего выражения:
Тогда
в 3 и 4 строках описка , второй раз написан корень((a-3)/2) , a нужно корень((a+3)/2)
спасибо, исправил
Похожие вопросы
Предмет: Русский язык,
автор: yahim
Предмет: Русский язык,
автор: ДашаLife
Предмет: Русский язык,
автор: графа
Предмет: Физика,
автор: IrinaLetyago
Предмет: Литература,
автор: oligumnowa