Предмет: Математика,
автор: vladasdus
докажите что при всех значениях переменных верно неравенство
Приложения:
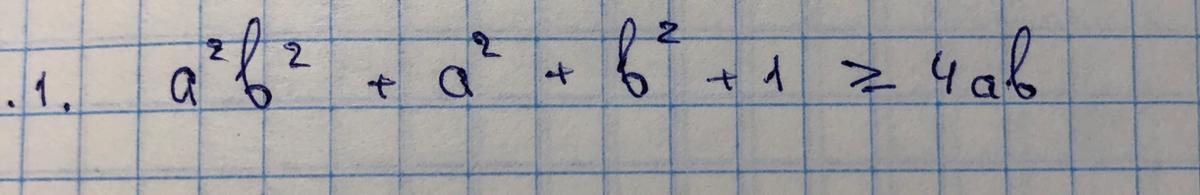
Ответы
Автор ответа:
1
Квадрат любого действительного числа всегда больше либо равен нулю.
Если (ab-1)²≥0 и (a-b)²≥0, то (ab-1)²+(a-b)²≥0 - ч.т.д
Похожие вопросы
Предмет: Английский язык,
автор: 2003Лерчик2003
Предмет: Русский язык,
автор: nika77755
Предмет: Русский язык,
автор: гьажи
Предмет: История,
автор: SariaaAvidzba
Предмет: Литература,
автор: Человек1501