Предмет: Геометрия,
автор: Fezantip
У трикутнику MNK MN=k, NK=m i MK=n, NL - бісектриса трикутника. Знайти довжину відрізка ML.
Приложения:
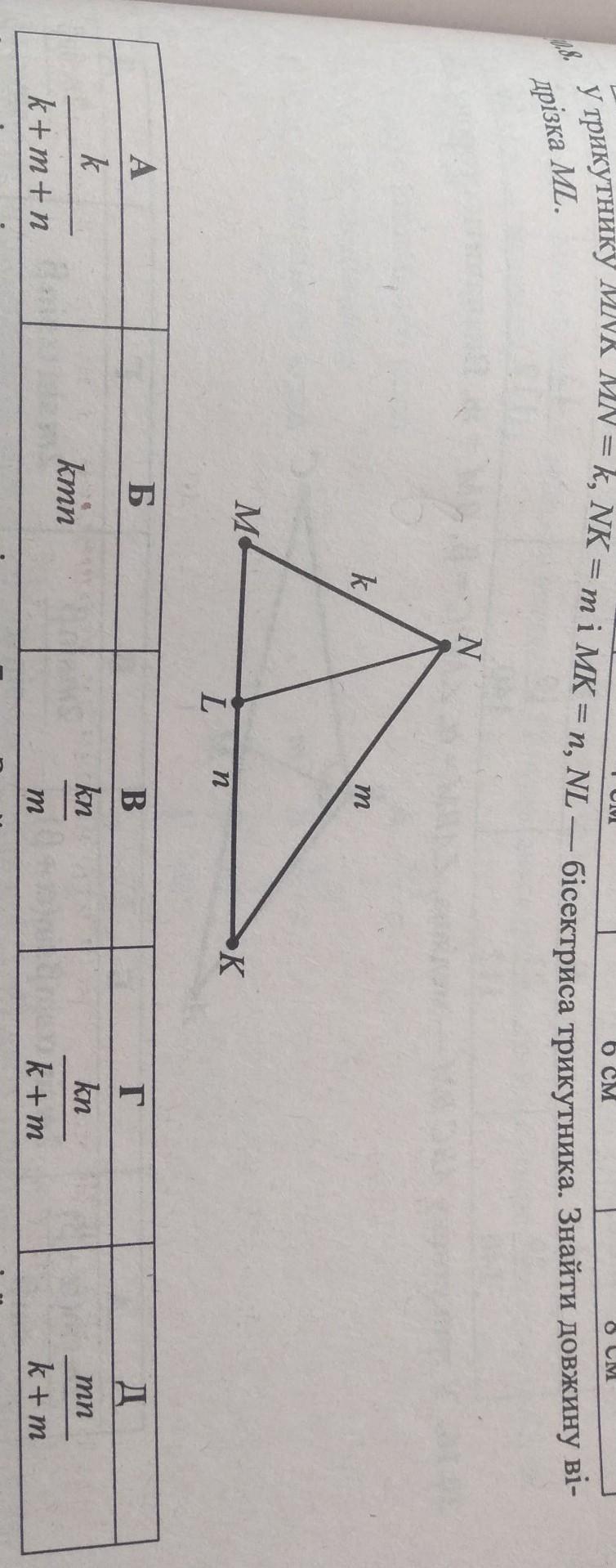
Ответы
Автор ответа:
1
Ответ:
Г )
Объяснение:
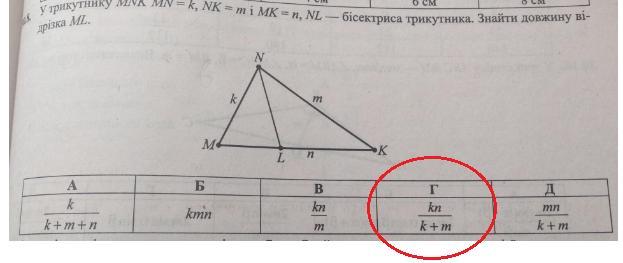
В треугольнике MNK, MN =k. NK= m, MK= n, NL - биссектриса треугольника . Найти длину отрезка ML.
По условию задан ΔMNK и в нем проведена биссектриса NL.
Свойство биссектрисы треугольника: биссектриса треугольника делит противолежащую стороны на отрезки пропорциональные длинам прилежащих сторон.
Тогда
Пусть искомый отрезок будет ML х ед. Тогда, если MK= n , то
KL = (n-x) ед.
Тогда получим пропорцию
В верной пропорции произведение крайних членов равно произведению средних членов пропорции.
Тогда получим ответ: Г)
#SPJ5
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kiler1111
Предмет: Английский язык,
автор: Dybitskaya83
Предмет: Русский язык,
автор: solnyshkina197
Предмет: Химия,
автор: salikhovaleyla
Предмет: Литература,
автор: kirill25evt