Предмет: Алгебра,
автор: kxrsxnch
решите пожалуйста, я бессилен
Приложения:
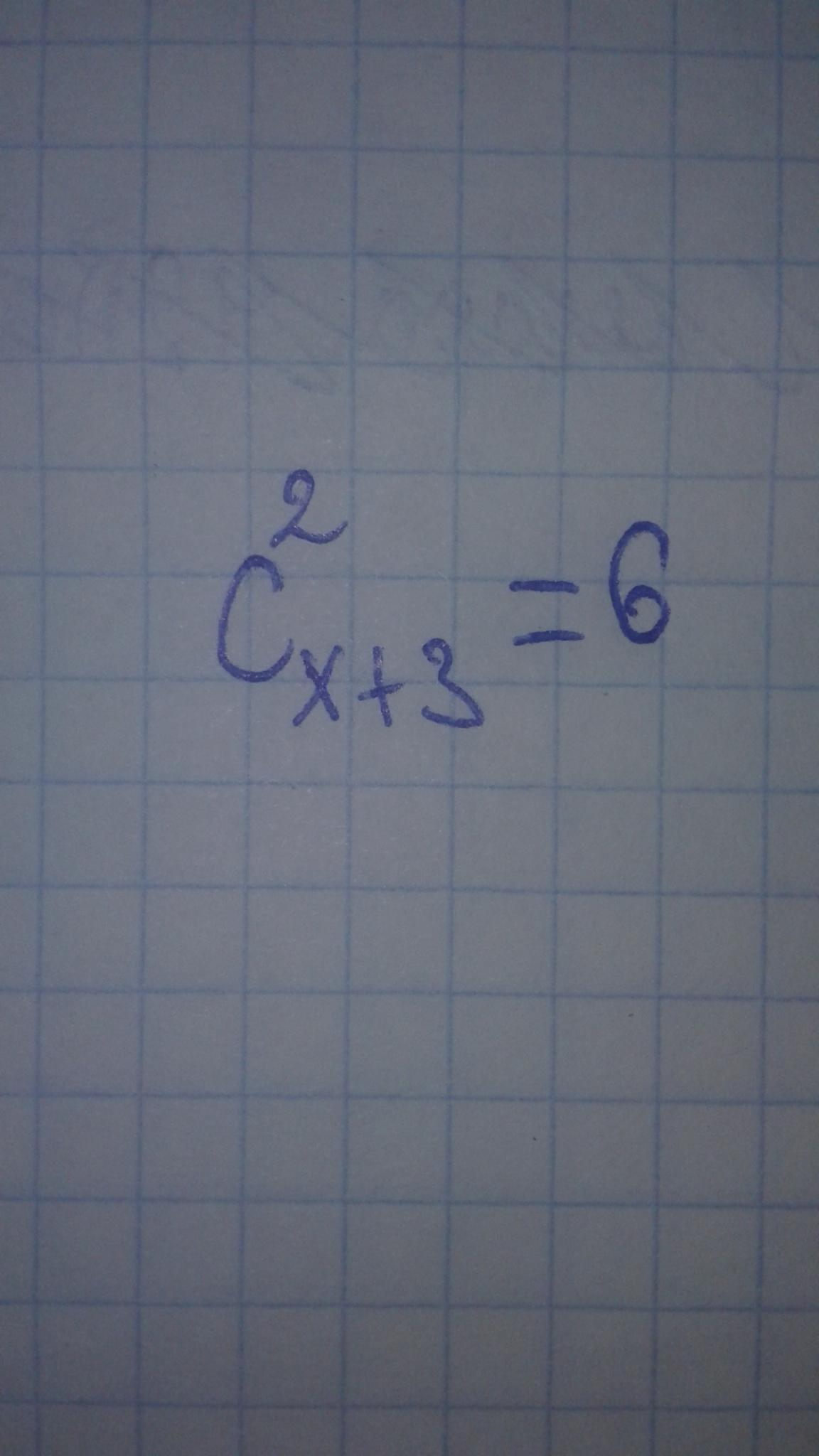
Ответы
Автор ответа:
1
Ответ:
ответ: х=1
Объяснение:
ограничения: x+3≥2 ⇔ x≥-1; x∈Z
x=-6 - не подходит под ограничения
Похожие вопросы
Предмет: Другие предметы,
автор: perfiloff2008
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: ekarchevskaya
Предмет: Математика,
автор: DimasSt25D
Предмет: Химия,
автор: flillen