Question

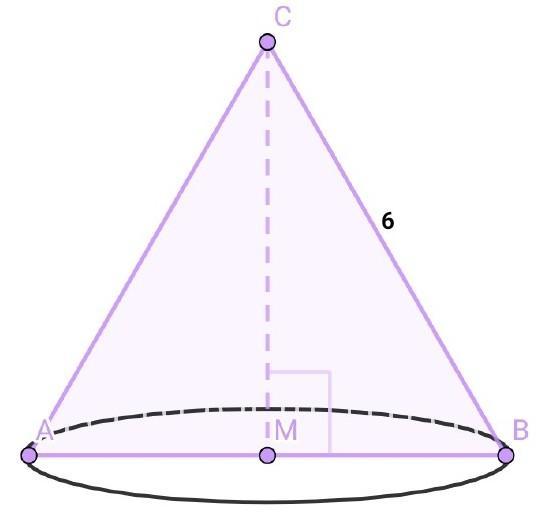
Образующая конуса равна 6. Осевое сечение конуса - равносторонний треугольник. Найти площадь поверхности конуса.

Answer 1

Дано:

Конус.

∆АВС — осевое сечение.

∆АВС — правильный.

СВ — образующая конуса = 6.

Найти:

S(боковой поверхности конуса) = ?

S(полной поверхности конуса) = ?

Решение:

Проведём высоту конуса СМ и рассмотрим отрезок ВМ — радиус основания конуса.

За счёт того, что ∆АВС — равносторонний, то ВМ = 0,5*СВ (по свойству равностороннего треугольника).

То есть —

ВМ = 0,5*6

ВМ = 3.

[Площадь боковой поверхности конуса равна произведению π, радиуса основания конуса и образующей конуса].

То есть —

S(боковой поверхности конуса) = π*ВМ*СВ

S(боковой поверхности конуса) = π*3*6

S(боковой поверхности конуса) = 18 (ед²)*π.

[Площадь полной поверхности конуса равна произведению π, радиуса и суммы радиуса основания и образующей конуса].

S(полной поверхности конуса) = π*ВМ*(ВМ + СВ)

S(полной поверхности конуса) = π*3*(3 + 6)

S(полной поверхности конуса) = π*3*9

S(полной поверхности конуса) = 27 (ед²)*π.

Ответ:

18 (ед²)*π.

27 (ед²)*π.