Question

Найдите все значения а, при каждом из которых уравнение
$\frac{x { }^{2} - 6x + a ^{2} - 8a }{x {}^{2} { - a}^{} } = 0$
имеет ровно два различных корня. ​

Answer 1

$x^2-6x+a^2-8a=0\\ \\ (x-3)^2+a^2-8a-9=0\\ \\ (x-3)^2=8a+9-a^2$

Уравнение имеет два различных корня когда его правая часть принимает положительные значения

$8a+9-a^2>0\\ \\ a^2-8a-9<0\\ \\ (a-4)^2-25<0\\ \\ |a-4|<5\\ \\ -5<a-4<5\\ \\ -1<a<9$

Теперь нужно учесть, что при некоторых $a$ уравнение может иметь два корня, но при этом один из корней не удовлетворяет ОДЗ

$x^2-a\ne 0\\ \\ x\ne \pm\sqrt{a}$

$(\sqrt{a})^2-6\sqrt{a}+a^2-8a=0\\ \\ a^2-6\sqrt{a}-7a=0\\ a=0;\\ a=9$

$(-\sqrt{a})^2-6\cdot (-\sqrt{a})+a^2-8a=0\\ \\ a^2+6\sqrt{a}-9a=0$

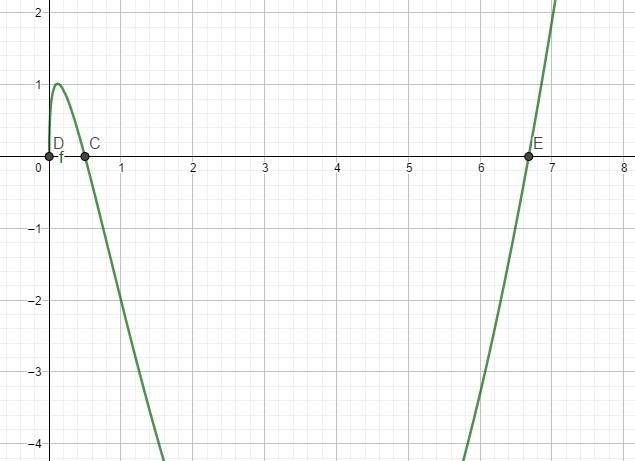
Корни этого уравнения смотрите на фото.

При $a \in (-1;0)\cup (0;1{,}5)\cup(1{,}5;6{,}68)\cup(6{,}68;9)$ уравнение имеет ровно два различных корня.