Предмет: Математика,
автор: moneylong41
решите неравенство пожалуйста .
Приложения:

Ответы
Автор ответа:
1
Дробно-рациональные и сложные неравенства высших степеней решаются с помощью метода интервалов.
Имеем функцию
1) Область допустимых значений (ОДЗ):
2) Ноль функции:
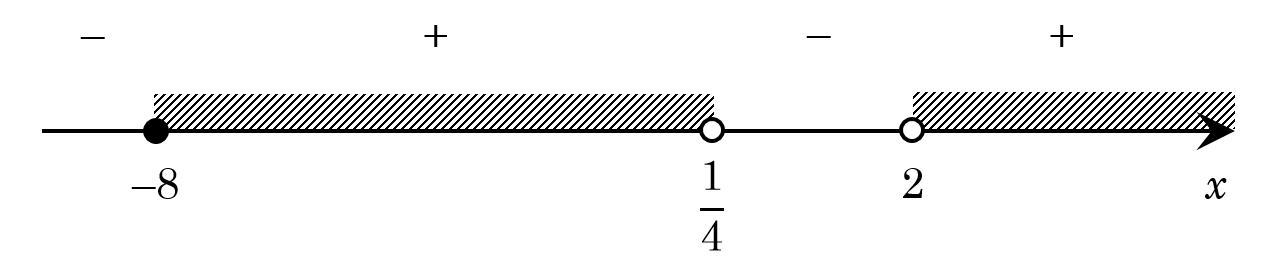
3) Изобразим координатный луч, отметим ноль функции и ОДЗ, и найдем значение функции на каждом интервале (см. рисунок).
4) Все значения, удовлетворяющие , объединим в промежуток:
Ответ:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: 1001сказка
Предмет: Українська мова,
автор: kamaewakatya
Предмет: Русский язык,
автор: innessaprikul
Предмет: Обществознание,
автор: andreipro007
Предмет: Физика,
автор: Сергей22800711