Question

Помогите пожалуйста, осталось 40 минут
1. Найти производную функции: y= cos 7x +log2(x5-3x) 2. Вычислить площадь фигуры, ограниченной осью абсцисс и параболой у= -x2+5x-6.

Answer 1

Найти производную функции: y= cos 7x +log2(x5-3x) 2. Вычислить площадь фигуры, ограниченной осью абсцисс и параболой у= -x2+5x-6.

Пошаговое объяснение:

1) y' = (cos7x +log(2)(x⁵-3x) )' =-7sin7х+ 1*(2x-3)/ ( (х²-3х)Ln2)=

=-7sin7х+ (2x-3)/ ( (х²-3х)Ln2).

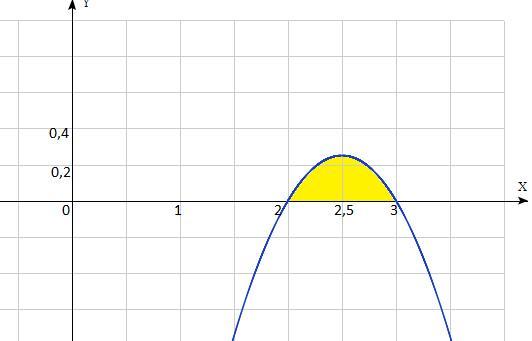
2)у= -x²+5x-6, ось ох.

у= -x²+5x-6, парабола ветви вниз. Координаты вершины х₀=-в/2а,

х₀=-5/(-2)=2,5  , у₀=0,25 .

Точки пересечения с ох, у=0 :-x²+5x-6=0 или    

x²-5x+6=0.   По т Виета х₁+х₂=5  ,х₁*х₂=6 . Значит х₁=2, х₂=3 и пределы интегрирования  от 2 до 3:

S=∫(-x²+5x-6))dx=(-х³/3+5х²/2-6х) |  =

(-3³/3+5*3²/2-6*3) -(-2³/3+5*2²/2-6*2) =

=-9+22,5-18+8/3-10+12=

=-37+34,5+8/3=1/6