Предмет: Математика,
автор: MrMice
Вычислить длины дуг кривых
Приложения:
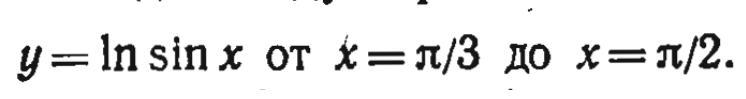
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Другие предметы,
автор: karina1998mus
Предмет: Русский язык,
автор: ziyarats
Предмет: Английский язык,
автор: Katerina286
Предмет: География,
автор: nastasyatokareva