Предмет: Геометрия,
автор: yrodkondabarov
Апофема правильной четырехугольной пирамиды наклонена плоскости основания под углом 45°. Высота пирамиды 6 см. Найти ее объем.
Ответы
Автор ответа:
0
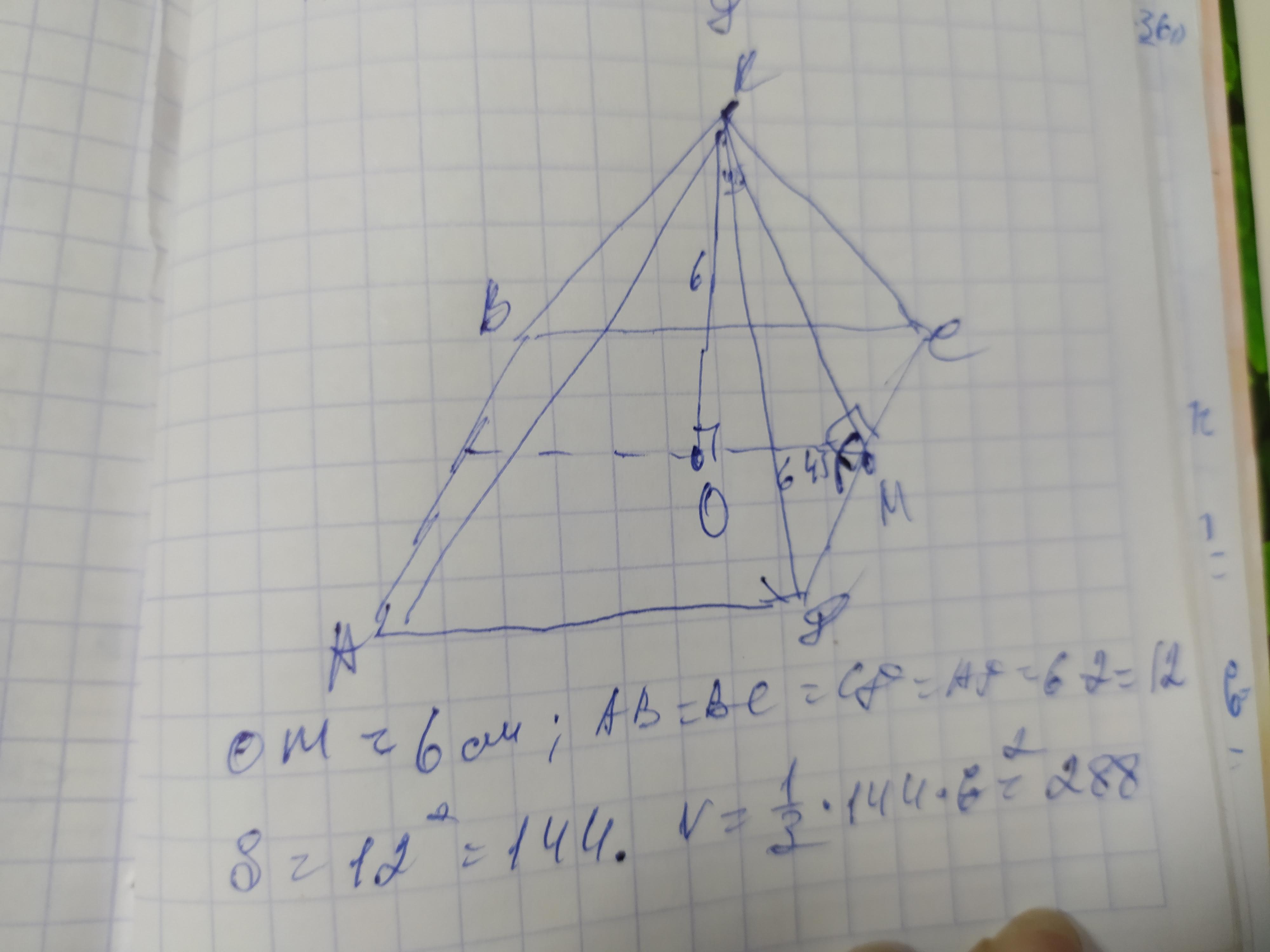
Обозначим вершины пирамиды АВСД, высоту КО, а апофему КМ. Соединим точки О и М и получим прямоугольный треугольник КМО, в котором высота КО и ОМ - катеты, а КМ - гипотенуза. Сумма острых углов прямоугольного треугольника составляет 90° и если угол КМО=45°, то угол МКО=90-45=45°. Этот треугольник равнобедренный, поэтому КО=МО=6см. В основании правильной четырёхугольной пирамиды лежит квадрат. Если МО=½ ВС, поэтому АВ=ВС=СД=АД=6×2=12см
Sосн=а², где а- сторона основания. Найдём по этой формуле площадь основания: S=12²=144см²
Теперь найдём объем пирамиды по формуле: V=⅓×Sосн×KO=⅓×144×6=288см³
ОТВЕТ: V=288см³
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: жен14ка
Предмет: Английский язык,
автор: aikabana
Предмет: Русский язык,
автор: ilya8920
Предмет: Геометрия,
автор: kerovr19titan
Предмет: Математика,
автор: нйшщвдчттч