Question

1.Дан цилиндр с радиусом основания 4см, диагональ осевого сечения равна 10см. Найдит: а)высоту цилиндра, б) площадь осевого сечения.
2. Вычислите боковую и полную поверхности конуса, образующая которого равна 20 см, а радиус основания 4 см.
Помогите пожалуйста!​

Answer 1

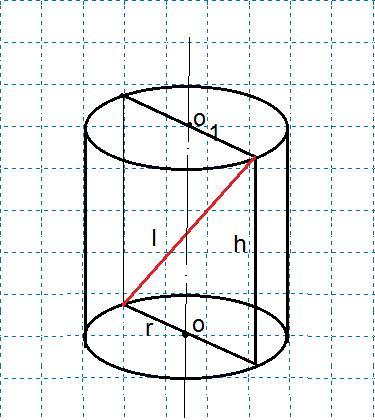
1. Высота цилиндра равна (по теореме Пифагора) h=√(l²-D²), где l - диагональ осевого сечения, а D - диаметр основания цилиндра.

1) 4×2=8 см - диаметр цилиндра

2) √(10²-8²)=√36=6 см - высота цилиндра

Площадь осевого сечения (прямоуг.) находим по формуле S=Dh.

3) 6×8=48 см² - площадь осевого сечения (см. рис в приложении)

2. Площадь боковой поверхности конуса находится по формуле S(b) = πRL, где R - радиус основания, а L - образующая.

1) 3,14×4×20=251,2 см² - площадь боковой поверхн. цилиндра

Полная площадь цилиндра находится по формуле S(p) = πRL + πR², где πR² - площадь основания (круга).

2) 3,14×4²=50, 24 см² - площадь основания

3) 251,2+50,24=301,44 см² - полная площадь цилиндра