Предмет: Алгебра,
автор: srodionov2001
Помогите пожалуйста решить, 4 любых из этих примеров. Пожалуйста
Приложения:
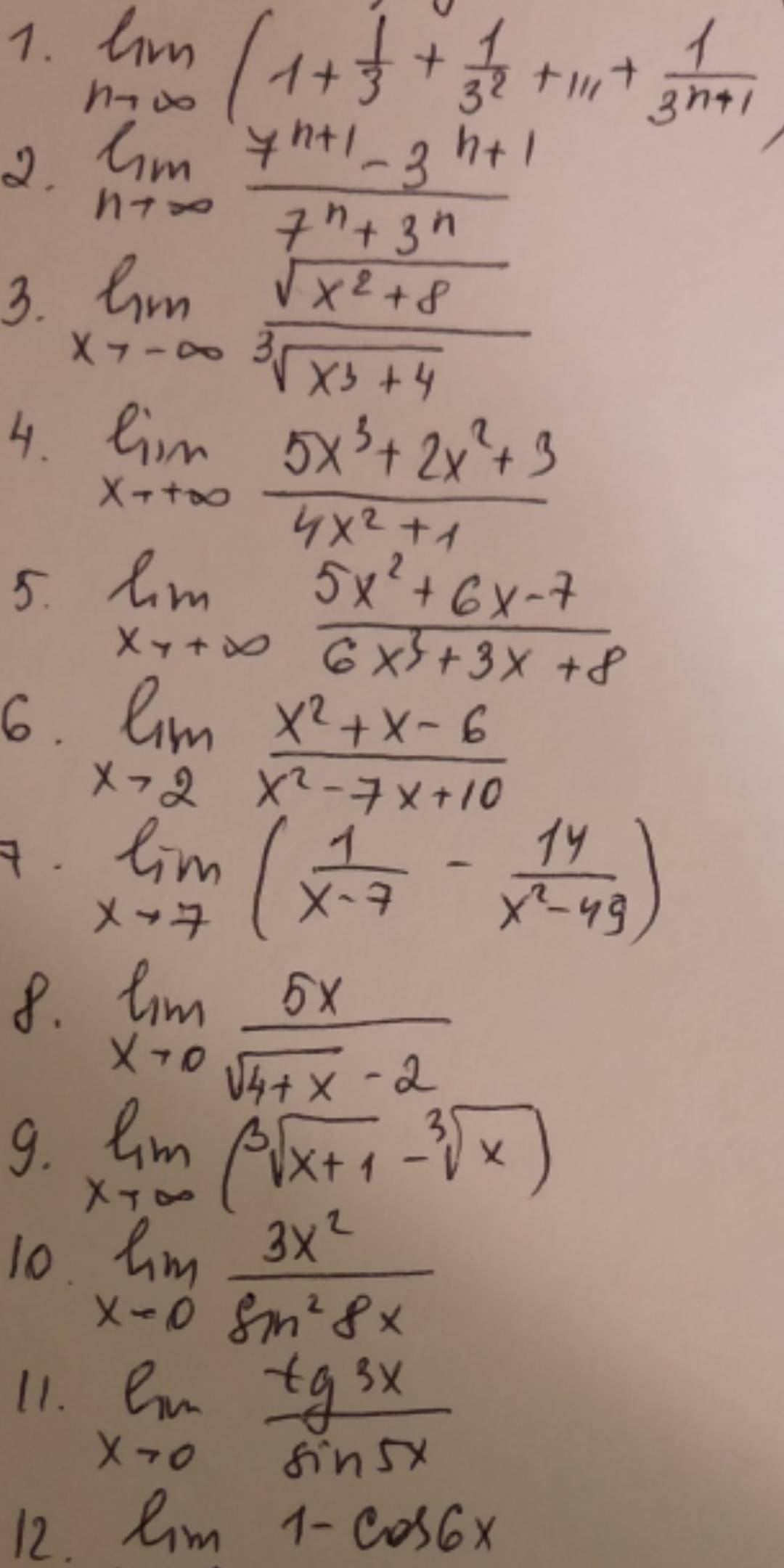
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: anel0202
Предмет: Русский язык,
автор: кирусик2304
Предмет: Русский язык,
автор: ДМ0
Предмет: Математика,
автор: knutika
Предмет: Литература,
автор: fadesesaa