Предмет: Математика,
автор: sanekbikbulatov
Вычислить производную функции y= 4x-3x^2 / x^3-1
Приложения:
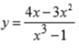
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
используем
где у нас будет u = (4x-3x²); v = (x³-1)
приведем все подобные в числителе и получим
Автор ответа:
1
Ответ:
Пошаговое объяснение:
(u/v)'=(u'v-uv')/v^2
y'=((4-6x)*(x^3-1)-(4x-3x^2)*3x^2) /(x^3 -1)^2 =
((4x^3-4-6x^4+6x-(12x^3-9x^4)) /(x^3-1)^2 =
(4x^3-4-6x^4+6x-12x^3+9x^4) /(x^3-1)^2=
(3x^4-8x^3+6x-4) /((x^3 -1)^2
Похожие вопросы
Предмет: Русский язык,
автор: narjan07
Предмет: Другие предметы,
автор: Ирина1984
Предмет: Українська мова,
автор: klmn123
Предмет: Литература,
автор: alikakovre
Предмет: Алгебра,
автор: TheInfoster