Предмет: Математика,
автор: victor785
исследовать на сходимость ряд
Приложения:
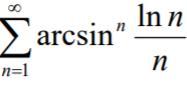
Ответы
Автор ответа:
0
Арксинус непрерывен на всей области определения. Тогда:
Тогда, по признаку Коши, ряд сходится
Автор ответа:
0
Ответ:
ряд сходится
Пошаговое объяснение:
используем радикальный признак Коши:
0<1, значит ряд сходится
Похожие вопросы
Предмет: Русский язык,
автор: popovaolga75
Предмет: Русский язык,
автор: xillikАня
Предмет: Русский язык,
автор: kariwenka99
Предмет: Математика,
автор: senyanoskov98