Предмет: Алгебра,
автор: parnishaindk
Найдите площадь фигуры, ограниченной линиями: f(x) = 2+x-x^2, ось OX
Ответы
Автор ответа:
1
Приложения:
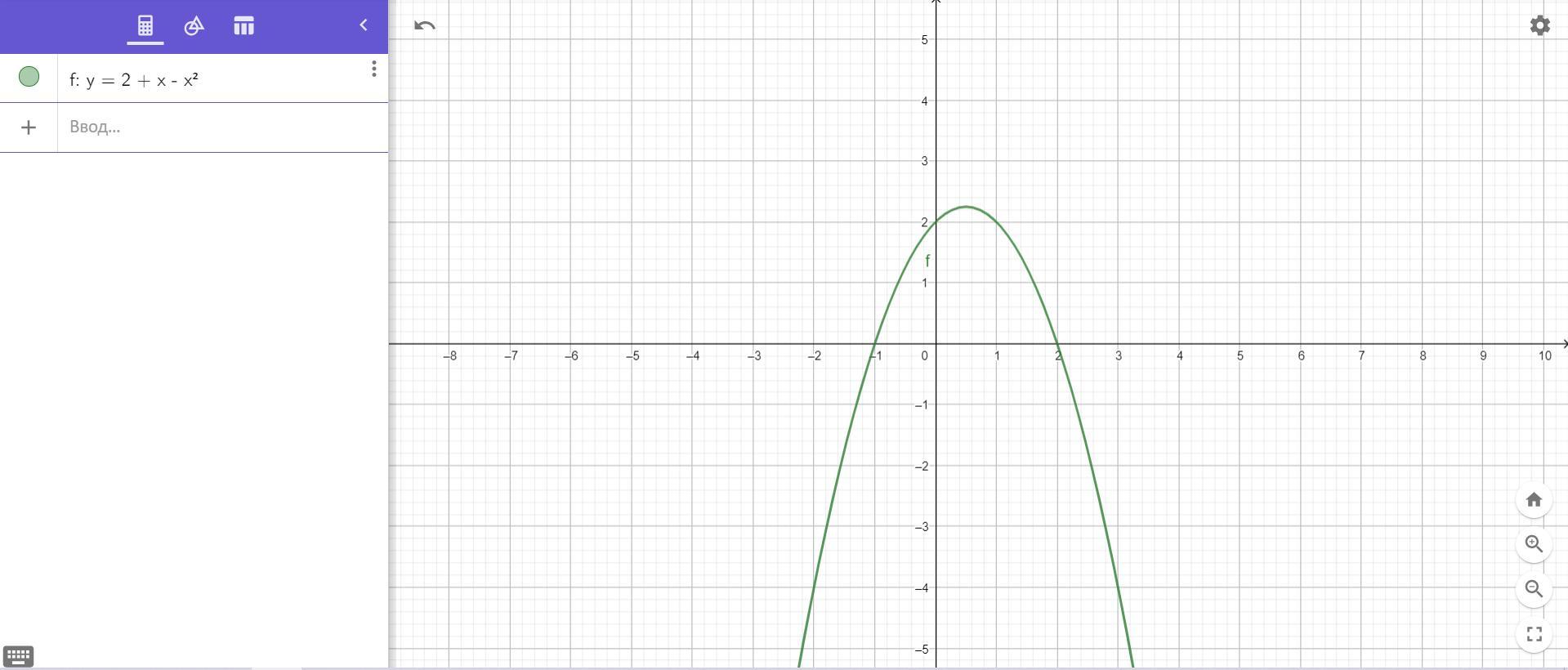
Похожие вопросы
Предмет: Русский язык,
автор: Марина01021974
Предмет: Русский язык,
автор: saarik
Предмет: Русский язык,
автор: Mash15
Предмет: Химия,
автор: Gnsim
Предмет: История,
автор: masterестьже