Предмет: Алгебра,
автор: iradimitr2009
Помогите решить пределы не применяя правила Лопиталя. Немного не понятно как это делать
Приложения:
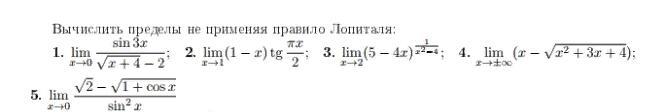
Ответы
Автор ответа:
0
Ответ:
2.
5.
Объяснение:
2. Выполняем замену y=1-x => x=1-y
3. В условии, скорее всего ошибка. Должно быть
5. Умножаем числитель и знаменатель на
Похожие вопросы
Предмет: Русский язык,
автор: олежеки
Предмет: Русский язык,
автор: LikaSaSha
Предмет: Русский язык,
автор: NightBreeze1
Предмет: Алгебра,
автор: igor543
Предмет: Математика,
автор: сойкан2
sin 3x / 3x = 1 ну и ответ уже есть