можно с подробным решением
и отбор корней вообще не ясен
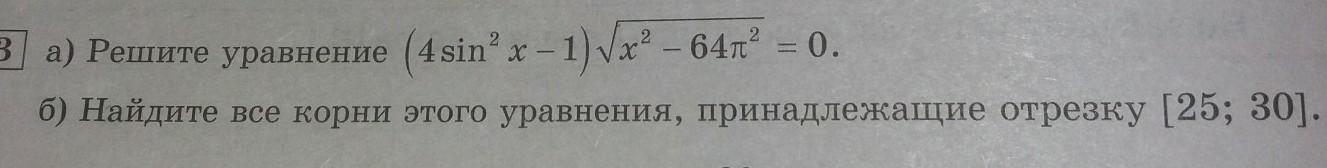
Ответы
Ответ:
8П; 49П/6; 53П/6; 55П/6
Объяснение:
Найти корни на отрезке [25; 30] ≈ [7,96П; 9,55П]
И в скобках, и под корнем - разности квадратов. Раскладываем.
Теперь можно приравнять к 0 каждую из скобок.
1) 2sin x - 1 = 0
sin x = 1/2
x = П/6 + 2Пk
В отрезок [7,96П; 9,55П] попадает корень:
x1 = П/6 + 8П = 49П/6 ≈ 8,17П
x = 5П/6 + 2Пk
В отрезок [7,96П; 9,55П] попадает корень:
x2 = 5П/6 + 8П = 53П/6 ≈ 8,83П
2) 2sin x + 1 = 0
sin x = -1/2
x = -П/6 + 2Пk
Пробуем подобрать корни
x = -П/6 + 8П ≈ -0,17П + 8П = 7,83П < 7,96П
x = -П/6 + 10П ≈ -0,17П + 10П = 9,83П > 9,55П
В отрезок [7,96П; 9,55П] не попадает ни один корень.
x = -5П/6 + 2Пk
В отрезок [7,96П; 9,55П] попадает корень:
x3 = -5П/6 + 10П = 55П/6 ≈ 9,17П
3) x - 8П = 0
x4 = 8П - попадает в отрезок [7,96П; 9,55П].
4) x + 8П = 0
x = 8П - не попадает в отрезок [7,96П; 9,55П].