Предмет: Математика,
автор: schok716
Срочно помогите сделать, плачу 15 баллов!!!!!
Приложения:
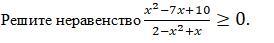
Ответы
Автор ответа:
1
| : (-1)
Дробь может быть меньше нуля в двух случаях:
x² - 7x + 10 = 0
D = (-7)² - 4*10 = 49 - 40 = 9 = 3²
x² - x - 2 = 0
D = (-1)² - 4*(-2) = 1 + 8 = 9 = 3²
Т.к. на 0 делить нельзя ⇒ х ≠ -1 и х ≠ 2
Ответ: х∈(-1;2)∪(2;5]
Похожие вопросы
Предмет: Русский язык,
автор: дашкоб
Предмет: Русский язык,
автор: Ксения080302
Предмет: Русский язык,
автор: Спартак1922
Предмет: Математика,
автор: KiscaBrisca1
Предмет: География,
автор: tatyanabyk