Предмет: Математика,
автор: alenamotina9
Исследовать на сходимость ряд
Приложения:
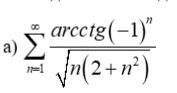
Ответы
Автор ответа:
1
Ответ:
Абсолютно сходится
Пошаговое объяснение:
Исследуем на сходимость ряд, состоящий из модулей слагаемых исходного ряда:
Будем использовать признак сравнения, а именно будем сравнивать этот ряд (с точностью до множителя перед знаком суммы) с
Посчитаем предел отношения членов этих рядов:
Этот предел конечный и не равен 0, значит, ряды сходятся или расходятся одновременно. Так как второй ряд имеет вид , где p>1, то он сходится, а значит сходится и исходный ряд, причем абсолютно.
Похожие вопросы
Предмет: Русский язык,
автор: veraglotova77
Предмет: Английский язык,
автор: katya727
Предмет: Русский язык,
автор: SashenkaCool
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: Emailmaksimko