Предмет: Алгебра,
автор: Кристина2429
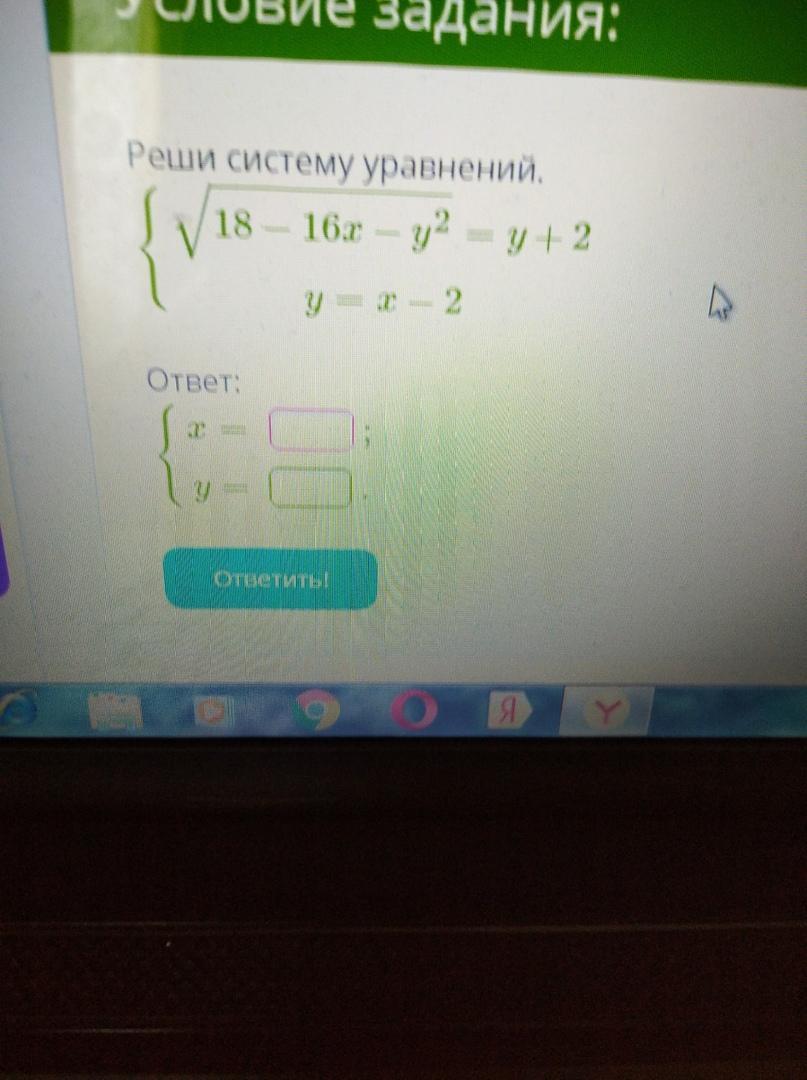
Помогите пж с алгеброй
Приложения:
Ответы
Автор ответа:
1
Ответ:
{(1; -1)}
Объяснение:
Дана система
Область допустимых значений: 18-16·х-у²≥0 и у+2≥0.
Проверим ОДЗ: 18-16·1-(-1)²=1>0 и -1+2=1>0 - условия выполняются.
Похожие вопросы
Предмет: Русский язык,
автор: irinaksl
Предмет: Русский язык,
автор: savchienkon
Предмет: Русский язык,
автор: Krislomlop
Предмет: Биология,
автор: shuhratok2000