Предмет: Геометрия,
автор: kolisomacaronu2
знайти координати четвертої вершини паралелограма abcd якщо дано координати трьох вершин а (2;1;3) c (-2;1;5) d (-1;2;1)
Ответы
Автор ответа:
3
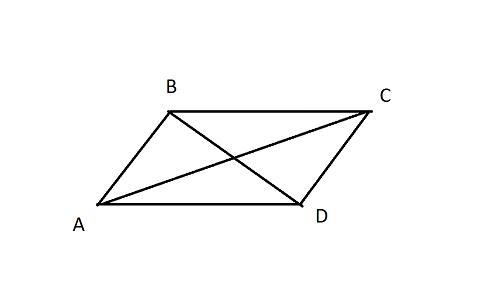
Диагонали точкой пересечения делятся пополам.
Тогда пусть т.О - точка пересечения диагоналей, найдем её как середину AC:
Точка О(0;1;4)
Тогда пусть B(x;y;z), зная что т.О - середина диагоналей найдем через диагональ BD координаты B:
Координаты точки
Приложения:
kolisomacaronu2:
Спасибо Огромное )))
Похожие вопросы
Предмет: Русский язык,
автор: hoopoty123sis
Предмет: Английский язык,
автор: KateBlackRose
Предмет: Английский язык,
автор: irakudelinalovaaaa
Предмет: Математика,
автор: vladik2a
Предмет: Математика,
автор: Krishtop