Предмет: Алгебра,
автор: karl160
1/x+1<2/x-3
Помогите решить, я вообще не понимаю.
nikebod313:
(x + 1) и (x - 3) в знаменателях дробей стоят?
да
Метод интервалов для сложных (дробно-рациональных) неравенств:
1) Делаете справа единую дробь, слева 0.
2) Находите ОДЗ.
3) Находите нули числителя (если такие есть).
4) Отмечается знак дроби на каждом интервале числовой оси абсцисс.
5) Записываете промежуток, которому соответствует данное неравенство.
1) Делаете справа единую дробь, слева 0.
2) Находите ОДЗ.
3) Находите нули числителя (если такие есть).
4) Отмечается знак дроби на каждом интервале числовой оси абсцисс.
5) Записываете промежуток, которому соответствует данное неравенство.
спасибо)
Вам решить?
желательно именно решение увидеть
чтоб я запомнил
Хорошо.
Ответы
Автор ответа:
1
Ответ: см фото.
Объяснение:
Приложения:

Автор ответа:
0
1) Сведем дробно-рациональное неравенство к виду
Домножим обе части неравенства на , при этом изменим знак неравенства на противоположный:
2) Найдем область допустимых значений (ОДЗ):
3) Найдем нули функции
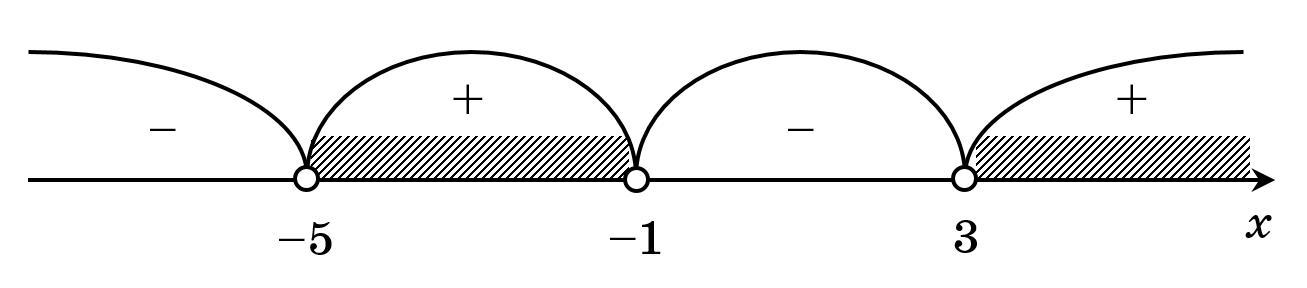
4) Обозначим на координатной прямой нули и ОДЗ функции , найдем знак функции на каждом промежутке (см. вложение), подставляя из выбранного промежутка некоторое значение (знак "+", если
, и "–", если
).
5) Объединим все полученные промежутки со знаком "+", поскольку
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: mentys85
Предмет: Русский язык,
автор: artandreev
Предмет: Другие предметы,
автор: creit
Предмет: Биология,
автор: anadtokasalnikova
Предмет: Математика,
автор: Mil12319