Предмет: Математика,
автор: margaritamorozova17
вычислите следующий интеграл
подробно пожалуйста
Приложения:
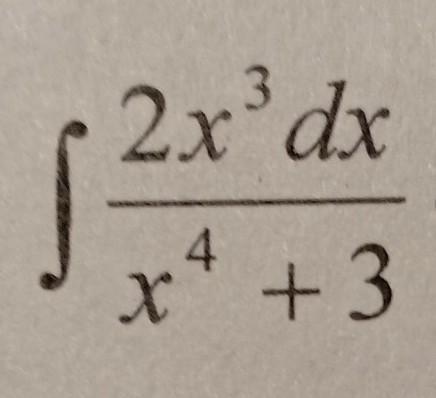
Ответы
Автор ответа:
1
Автор ответа:
0
Ответ:
-----------------------------------------------------------------------
Замена переменной
-----------------------------------------------------------------------
Похожие вопросы
Предмет: Русский язык,
автор: dmedomodedovo
Предмет: Английский язык,
автор: TRFan
Предмет: Қазақ тiлi,
автор: elegant65
Предмет: Математика,
автор: крис799
Предмет: Математика,
автор: annalex28