Предмет: Математика,
автор: ustinovat17
Пожалуйста, решите одно уравнение
Приложения:
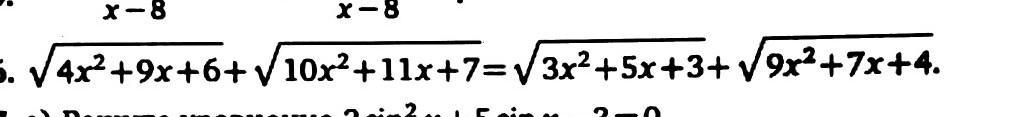
Ответы
Автор ответа:
0
Перепишем уравнение в виде , где вновь введенные переменные обозначают квадратные трехчлены в условии, читать по порядку.
Заметим, что . Перепишем уравнение:
. Возведем в квадрат:
, откуда
. Можем составить два квадратных уравнения (одинаковых):
, его корни
, второе
, те же корни, ведь они идентичны. Поэтому либо
, либо
;
Первый случай после подстановки не дает решений, второй случай дает корни . Оба корня подходят.
Ответ: -3, -1
Похожие вопросы
Предмет: Русский язык,
автор: sultasheva2004
Предмет: Русский язык,
автор: lallka228
Предмет: Русский язык,
автор: Tanyass
Предмет: Математика,
автор: суперкот8
Предмет: Математика,
автор: aleks561