Предмет: Математика,
автор: Nekromant22
Докажите тождество (см. вложение)
Приложения:
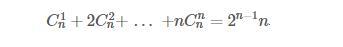
Ответы
Автор ответа:
1
Рассмотрим слагаемое ,
.
Это количество сочетаний из элементов по
, повторенное столько же раз.
Выстроим одну из комбинаций из элементов в строчку. Домножив на
, получим квадрат
элементов. То есть
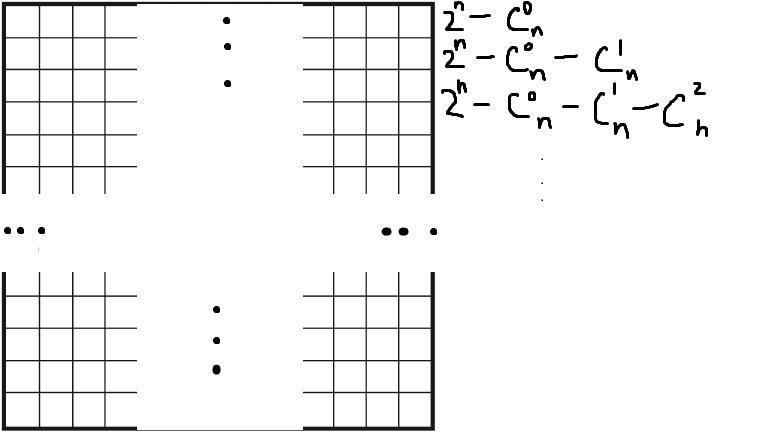
— это множество квадратов. Теперь построим квадратную таблицу
(см.рис)
В первой строке будут первые строчки большинства квадратов, кроме . Во второй строчке уже не будет
, поскольку квадраты
целиком умещаются в первой строчке. И т.д. Причем будет отсутствовать вычитаемое
, т.к. этот квадрат содержит все строчки.
Пусть искомая сумма . Сложив все строчки, получим
, поскольку
, перепишем сумму:
Приложения:
Автор ответа:
1
Ответ:
Пошаговое объяснение:в приложении
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: 68liza
Предмет: Українська мова,
автор: prizrak152
Предмет: Английский язык,
автор: EnglishStudent01
Предмет: Алгебра,
автор: arslanovaalina3
Предмет: Математика,
автор: DianaKotova167