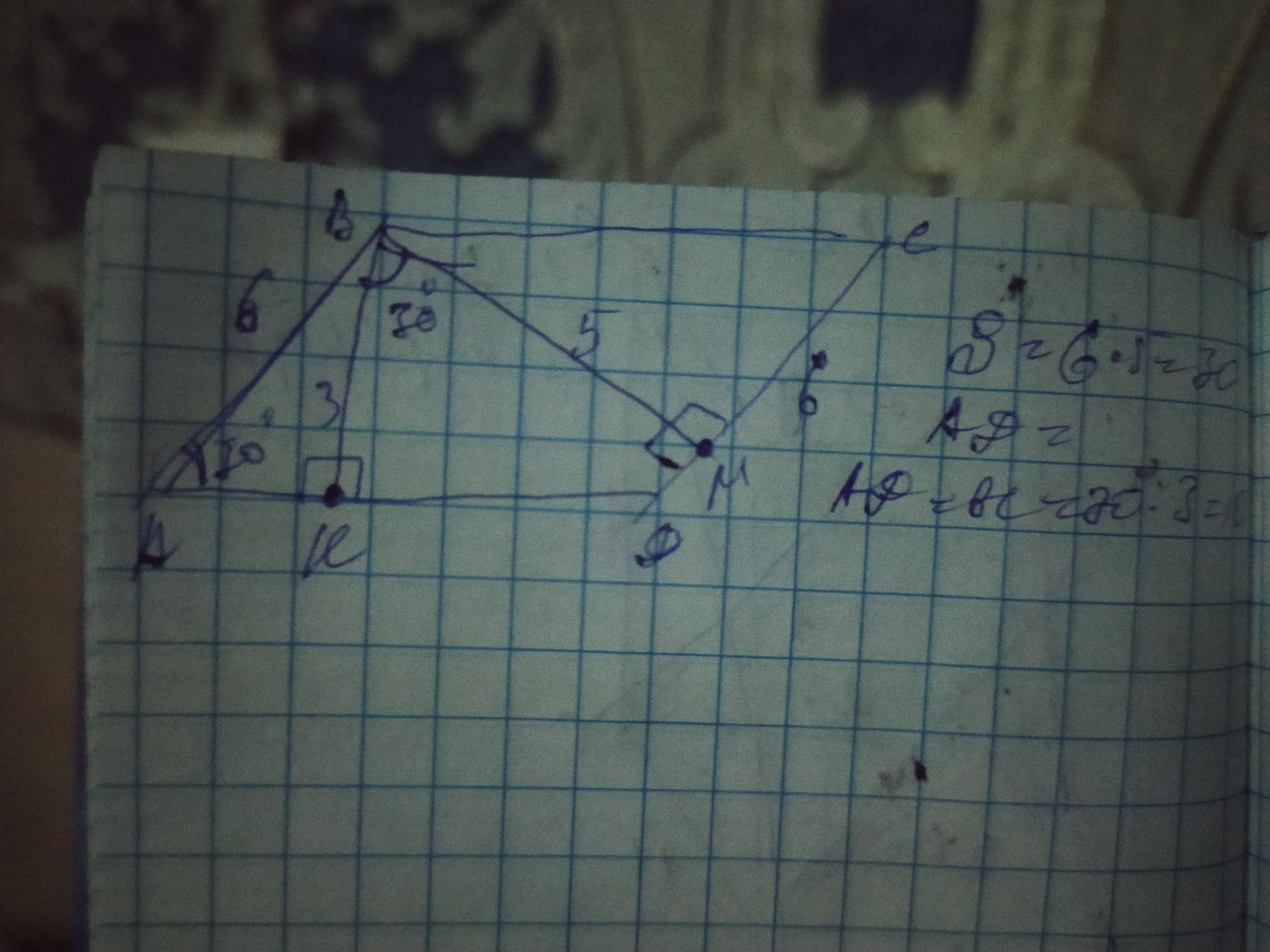
У паралелограмі АВСD з вершини тупого кута проведені висоти ВК і ВМ до сторін АD і DС відповідно. ВК = 3 см, ВМ = 5 см, КВМ = 30о. Знайдіть периметр паралелограма.
Ответы
Угол между двумя высотами параллелограмма проведёнными из тупого угла равнен острому углу параллелограмма. Следовательно угол КВМ=углу А=углу С=30°. Рассмотрим ∆АВК. Он прямоугольный. В нём АК и ВК - катеты, а АВ - гипотенуза. Так как угол А=30°, то катет ВК лежащий напротив него равен половине гипотенузы. Тогда гипотенуза АВ=2×3=6см
Итак: АВ=СД=6см
Площадь параллелограмма- это произведение его стороны и высоты проведённой к этой стороне. Найдём площадь параллелограмма по формуле:
S=СД×BM=6×5=30см²
Зная площадь параллелограмма и вторую высоту, найдём сторону, к которой проведена вторая высота, следуя формуле обратной нахождения площади: АД=ВС=S÷BK=30÷3=10см
Итак: АД=ВС=10см
Теперь найдём периметр параллелограмма, зная его стороны:
Р=2(6+10)=2×16=32см
ОТВЕТ: Р=32см