Предмет: Математика,
автор: Vector74
помогите решить этот пример каторый на картинке
Приложения:
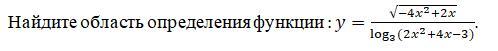
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: fanatCSKA
Предмет: Қазақ тiлi,
автор: Solnechnayazajka2003
Предмет: Русский язык,
автор: ket8512
Предмет: Химия,
автор: Ksenia17773