Предмет: Математика,
автор: 79315927192
Сложное неравенство ПОМОГИТЕ ПОЖАЛУЙСТА
Приложения:
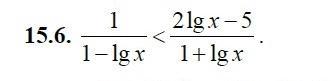
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1/(1 - lg x) < (2lg x - 5)/(1 + lg x)
Область определения:
{ x > 0
{ lg x ≠ 1; x ≠ 10
{ lg x ≠ -1; x ≠ 0,1
Замена lg x = y
1/(1 - y) < (2y - 5)/(1 + y)
1/(1 - y) - (2y - 5)/(1 + y) < 0
(1+y) / [(1-y)(1+y)] - (2y-5)(1-y) / [(1-y)(1+y)] < 0
[1+y - (2y-5)(1-y)] / [(1-y)(1+y)] < 0
[1+y + (2y-5)(y-1)] / [(1-y)(1+y)] < 0
(1+y+2y^2-5y-2y+5) / [(1-y)(1+y)] < 0
(2y^2 - 6y + 6) / [(1-y)(1+y)] < 0
2(y^2 - 3y + 3) / [(1-y)(1+y)] < 0
Попробуем найти корни числителя
y^2 - 3y + 3 = 0
D = 3^2 - 4*1*3 = 9 - 12 = -3 < 0
Числитель корней не имеет. Так как а = 1 > 0, то ветви направлены вверх, значит, он > 0 при любом у.
Поэтому его можно не учитывать.
1/[(1-y)(1+y)] < 0
y € (-oo; -1) U (1; +oo)
x € (0; 0,1) U (10; +oo)
Похожие вопросы
Предмет: Английский язык,
автор: ыолд
Предмет: Русский язык,
автор: natalicurlyженя
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: kedrovavarvara
Предмет: Алгебра,
автор: t0ha1337