Предмет: Алгебра,
автор: danilfolmer123
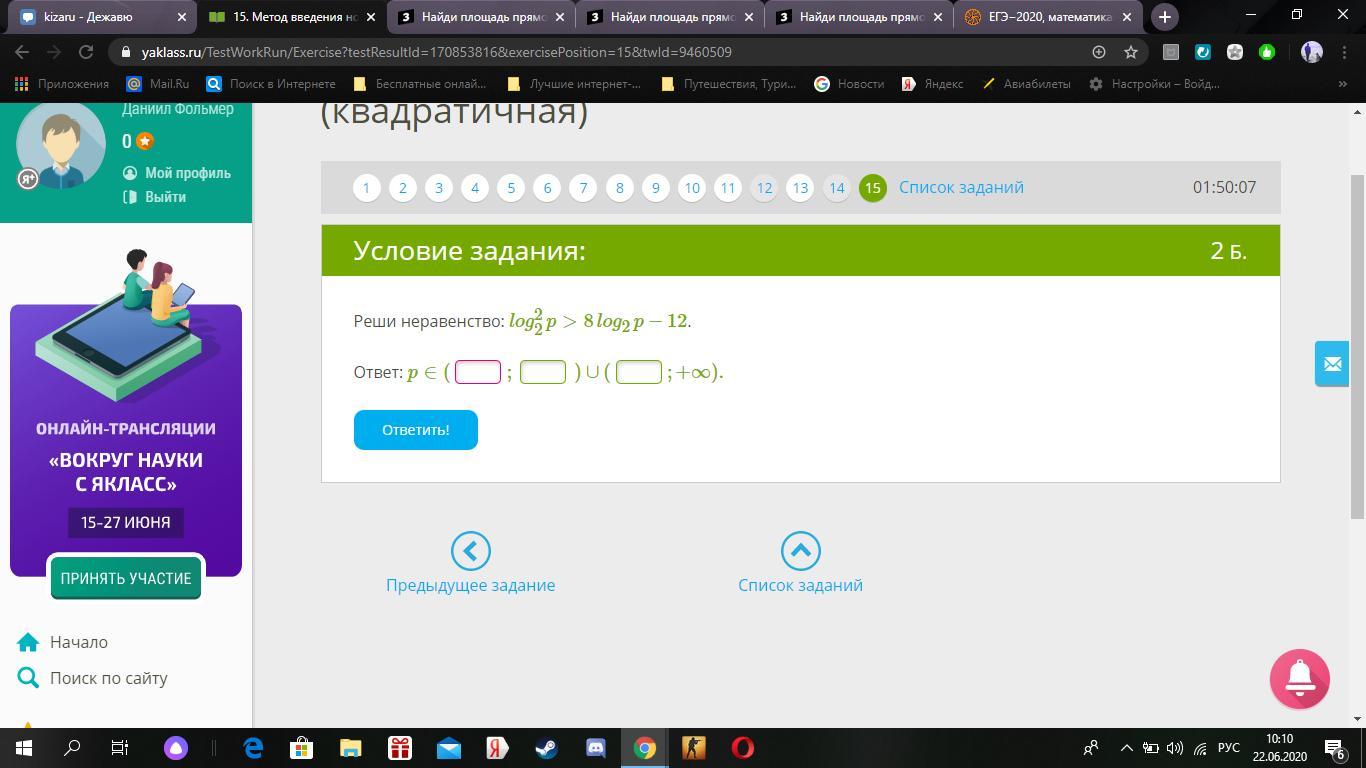
Реши неравенство: log^2/2p>8log2p−12. Приложен фаил.
Приложения:
Ответы
Автор ответа:
2
ОДЗ : p > 0
+ - +
______₀_____₀______ m
2 6
//////////// //////////////
Автор ответа:
3
Объяснение:
ОДЗ: p>0 ⇒ p∈(0;+∞).
Пусть log₂p=t ⇒
-∞__+__4__-__64__+__+∞
p∈(-∞;4)U(64;+∞).
Учитывая ОДЗ:
Ответ: p∈(0;4)U(64;+∞).
Похожие вопросы
Предмет: Українська мова,
автор: pulipusa
Предмет: Українська мова,
автор: Mala1234
Предмет: Другие предметы,
автор: berezinanati
Предмет: Математика,
автор: знания210