Предмет: Математика,
автор: katyakondrateva2003
Найти площадь фигуры, ограниченной параболой
Приложения:
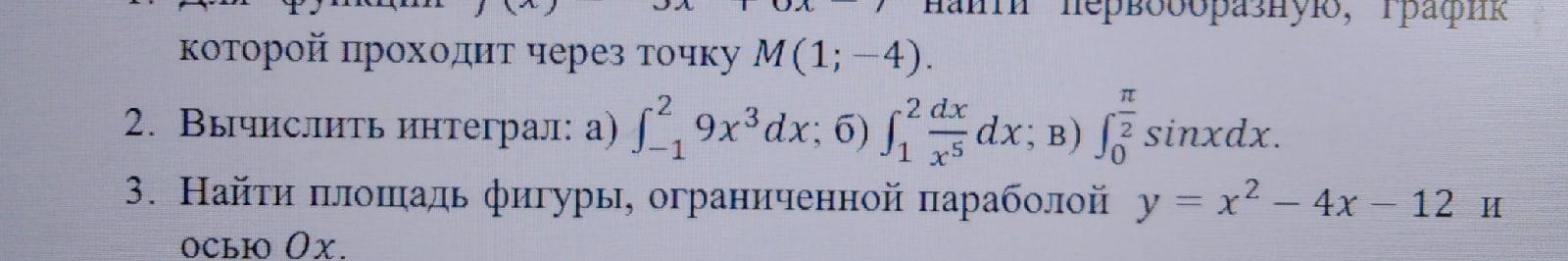
Аноним:
какая?
Найти площадь фигуры, ограниченной параболой =2−4−12и осью .
Ответы
Автор ответа:
1
Сначала ищем корни уравнения параболы, чтобы понять, где она пересекает ось ОХ:
Теперь берём интеграл от функции параболы на интервале от –2 до 6:
∫(x² – 4x – 12)dx =
= x³/3 – 2x² – 12x от –2 до 6
Площадь не может быть отрицательной, поэтому ответ будет со знаком «плюс»: 85⅓.
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
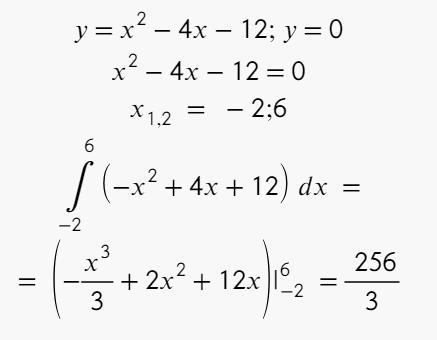
Похожие вопросы
Предмет: Русский язык,
автор: oksanamironova1
Предмет: Українська мова,
автор: anna268
Предмет: Русский язык,
автор: natalistepanov
Предмет: Алгебра,
автор: fanisrakhimov1