Предмет: Алгебра,
автор: Aleksspicen
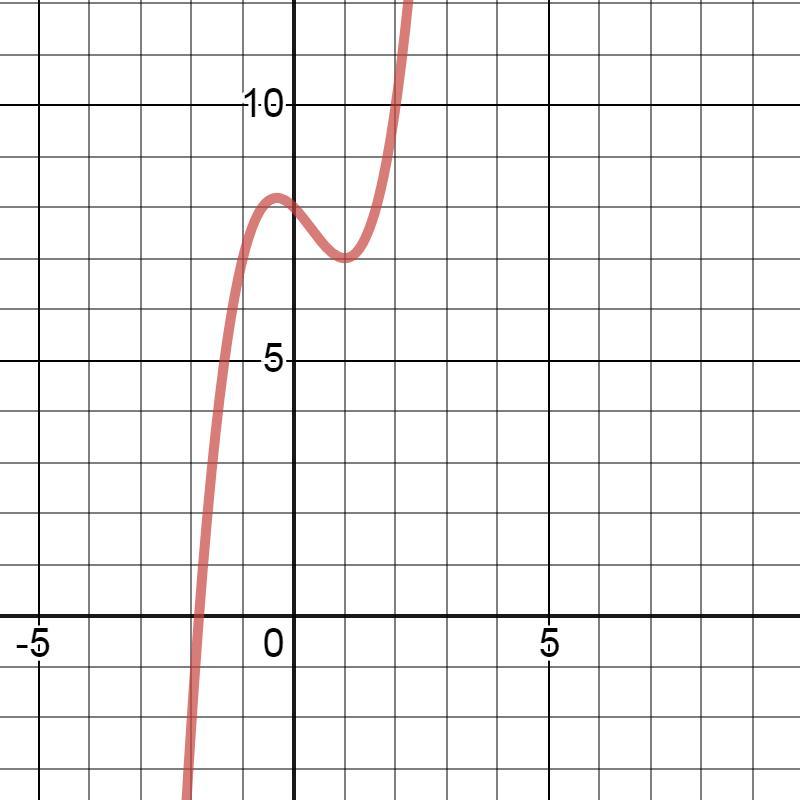
Найдите наименьшее значение функции y=x^3-x^2-x+8 на отрезке [0,4].
Aleksspicen:
На отрезке [0;4]
Ответы
Автор ответа:
1
Объяснение:
Ответ: y(1)=7.
Приложения:
Ну а с чего оно наименьшее то , а не наибольшее ? ))
А сорри - крайние точки посчитали - сорри ))
Наибольшее: у(4)=52.
Извините ещё раз )) Привык что вторую
производную ищут ...
производную ищут ...
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: alinakuleshova
Предмет: Русский язык,
автор: milkyw200
Предмет: Математика,
автор: zorinaksenia
Предмет: Математика,
автор: Detpoolplay