Предмет: Математика,
автор: ivelinahristovahrist
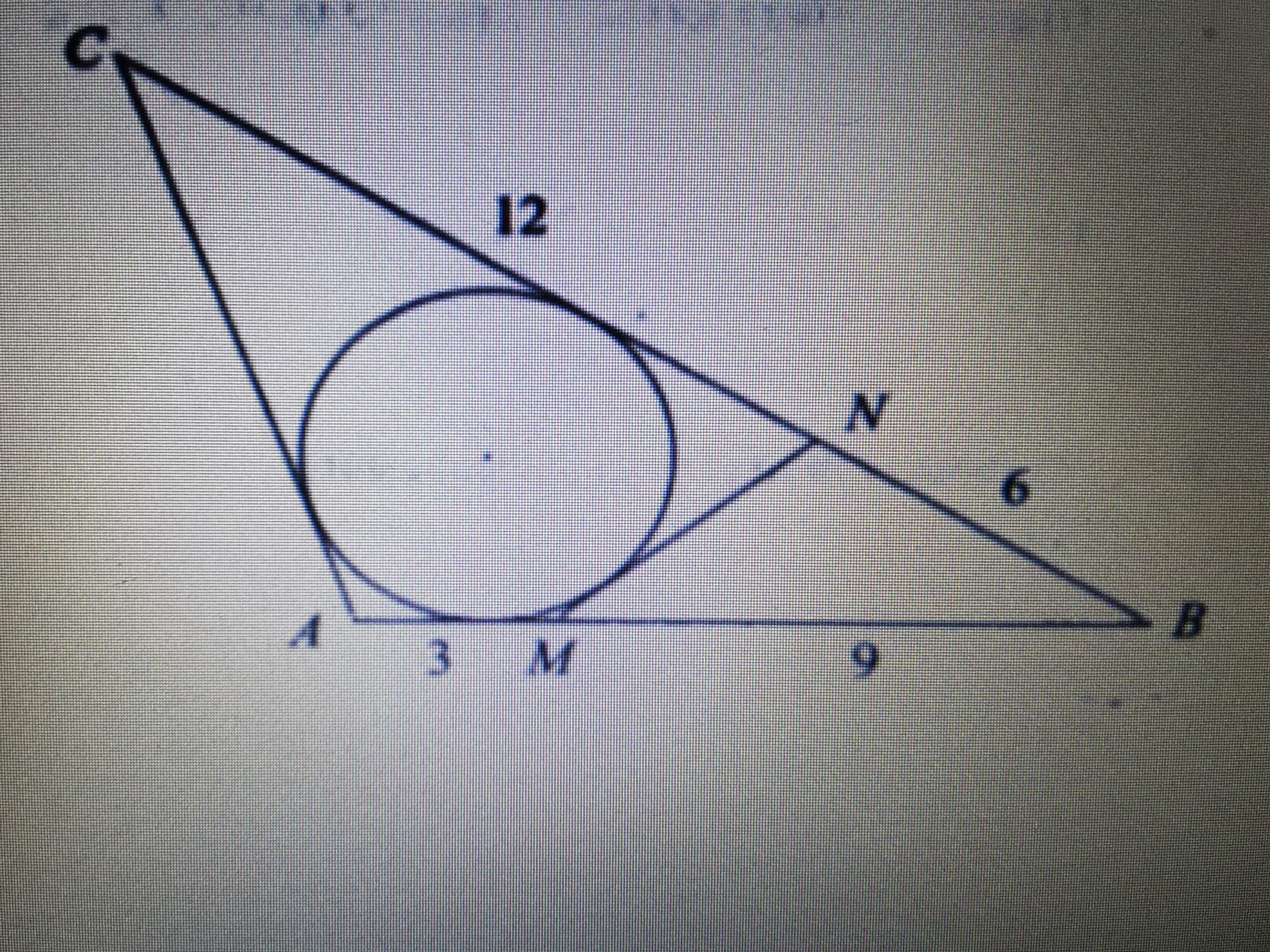
Помогите, пожалуйста! АC=?
Приложения:
Ответы
Автор ответа:
2
Четырехугольник AMNC можно описать вокруг окружности тогда и только тогда, когда суммы длин его противоположных сторон равны.
Значит, MN + АС = 3 + 12 = 15.
Пусть АС = х, MN = 15-х.
Далее используем формулу косинуса угла В из треугольников BMN и АВС.
(9² + 6² - (15 - х)²)/(2*9*6) = (12² + 18² - х²)/(2*12*18).
(81 + 36 - 225 + 30х - х²)/(2*9*6) = (144 + 324 - х²)/(2*12*18)
После сокращения и приведения подобных получаем квадратное уравнение х² - 40х + 300 = 0. Д = 1600 - 4*300 =400.
х1 = (40 - 20)/2 = 10, х2 = (40 + 20)/2 = 30.
Второе значение отбрасываем, так как оно больше суммы сторон.
Ответ: АС = 10.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: refat123456789
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Leragip
Предмет: История,
автор: drmrnkv
Предмет: Математика,
автор: rusya05