Можете, пожалуйста, решить 42 и 46
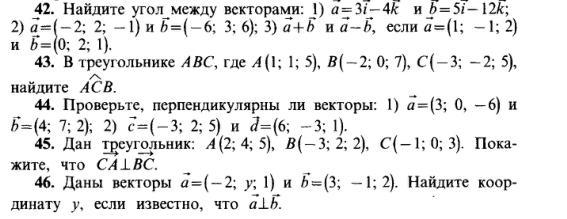
Ответы
Объяснение:
42)
1)а=3i-4k , а(3;0;-4), |а |=√( 3²+0²+ (-4)²)=5 ;
b=5i-12k ,в(5;0;-12) , |в|=√( 5²+0²+ (-12)²)=13.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними: а*в= |а|* |в|*cos∠(а;в) , cos∠(а;в)=(а*в): (|а|* |в|).
cos∠(а;в)=(3*5+0*0+(-4)*(-12) ): (5*13) ,
cos∠(а;в)=63: 65 , ∠(а;в)=arccos(63/65).
2) а(-2;2;-1), |а |=√( 4+4+ 1)=3 ;
в(-6;3;6) , |в|=√( 36+9+ 36)=9.
cos∠(а;в)=(12+6-6 ): (27) ,
cos∠(а;в)=4: 9 , ∠(а;в)=arccos(4/9).
3)а(1;-1;2), в(0;2;1) .тогда вектор
а+в(1;1;3) -координаты складывали ,и
а-в(1;-3;1) -координаты вычитали .
|а+в |=√( 1+1+9)=√11 ;
|а-в|=√( 1+9+ 1)=√11.
cos∠(а+в;а-в)=(1-3+3 ): √11² ,
cos∠(а+в;а-в)=1:11, ∠(а+в;а-в)=arccos(1/11).
46) а(-2;у;1), в(3;-1;2) .а⊥в.
Т.к вектора перпендикулярны , то скалярное произведение равно 0.
-6-у+2=0 , у=-4
46. Если скалярное произведение векторов равно нулю, то векторы перпендикулярны.
-2*3-у+1*2=0; у=2-6; у=-4
42. 1)(3;0;-4)*(5;0;-12)=15+48=63; Длина вектора а равна √(9+16)=5; вектора b равна √(25+144)=13 ; cosα=63/(5*13)=63/65; α=arccos(63/65)
2)(-2;2;-1)*(-6;3;6)=12+6-6=12; Длина вектора а равна √(4+4+1)√9=3; вектора b равна √(36+9+36)=9 ; cosα=12/(9*3)=4/9; α=arccos(4/9)
3) а+b=(1;-1;2)+(0;2;1)=(1;1;3)
а-b=(1;-3;1); (а+b)*(а-b)=(1;1;3)(1;-3;1)=1-3+3=1; Длина вектора а+b равна √(1+1+9)√11; вектора а-b равна √(1+9+1)=√11 ; cosα=1/(√11*√11)=1/11; α=arccos(1/11)
-6-у+2=0, y=-4