Предмет: Геометрия,
автор: gnomiha211
[30б]
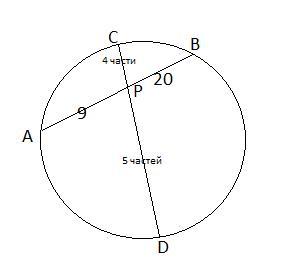
Хорды AB и CD пересекутся в точке P и хорду AB делит на два отрезка |AP|=9 и |BP|=20. Точка P делит хорду CD на два отрезка так, что отношение длин этих отрезков равно 4:5. Найдите длину меньшего отрезка.
Спаcибо !!
Ответы
Автор ответа:
1
Хорды AB и CD пересекутся в точке P и хорду AB делит на два отрезка |AP|=9 и |BP|=20. Точка P делит хорду CD на два отрезка так, что отношение длин этих отрезков равно 4:5. Найдите длину меньшего отрезка.
Объяснение:
Произведения длин отрезков каждой из хорд равны⇒
АР*РВ=СР*РD (*).
Учтем, что СР/РD=4/5 или СР=4/5*РD ( 4/5=0,8) , подставим все данные в (*).
9*20=0,8РD*РD , РD²=180:0,8=1800/8=225 , РD=15.
Найдем длину СР=4/5*РD , СР=0,8*15=12.
Длина меньшего отрезка 12
Приложения:
gnomiha211:
спасибо большое за ответ!
только в действии где 9/20= 0,8PD*PD не должно быть 9 ×20 ?
ничего, бывает) спасибо еще раз
Похожие вопросы
Предмет: Русский язык,
автор: ibb27
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: лутший23
Предмет: Математика,
автор: Viola2801
Предмет: Математика,
автор: Danik55511