Предмет: Алгебра,
автор: Qweeekg
[1] Найти наименьшие положительные периоды тригонометрической функции
Приложения:
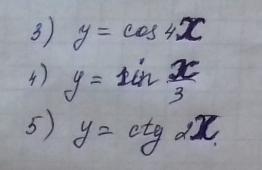
Ответы
Автор ответа:
2
Ответ:
Qweeekg:
Благодраю
Автор ответа:
0
Ответ:3)π/2; 4)6π; 5) π/2
Объяснение:Чтобы найти наименьший положительный период для синуса и косинуса, надо 2π поделить на коэффициент при х.
3) 2π/4=π/2
4) 2π/(1/3)=6π
Чтобы найти наименьший положительный период для тангенса и котангенса, надо π поделить на коэффициент при х.
5) π/2
Благодарю
Похожие вопросы
Предмет: Українська мова,
автор: урі
Предмет: Русский язык,
автор: cyik78
Предмет: Английский язык,
автор: elkhane
Предмет: Математика,
автор: lowetsAlecksei
Предмет: Математика,
автор: avatariyvika