Предмет: Алгебра,
автор: valera12121212212
Найти производную заданную неявно
Приложения:
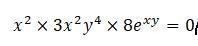
igorShap:
Уверены, что в правой части 0?
да
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: gdjgjv
Предмет: Русский язык,
автор: elena12101978
Предмет: Английский язык,
автор: Pomogiteludeplizz
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: Hackerywka