Предмет: Математика,
автор: stas28084
Пределы функций,помогите пожалуйста решить
Приложения:
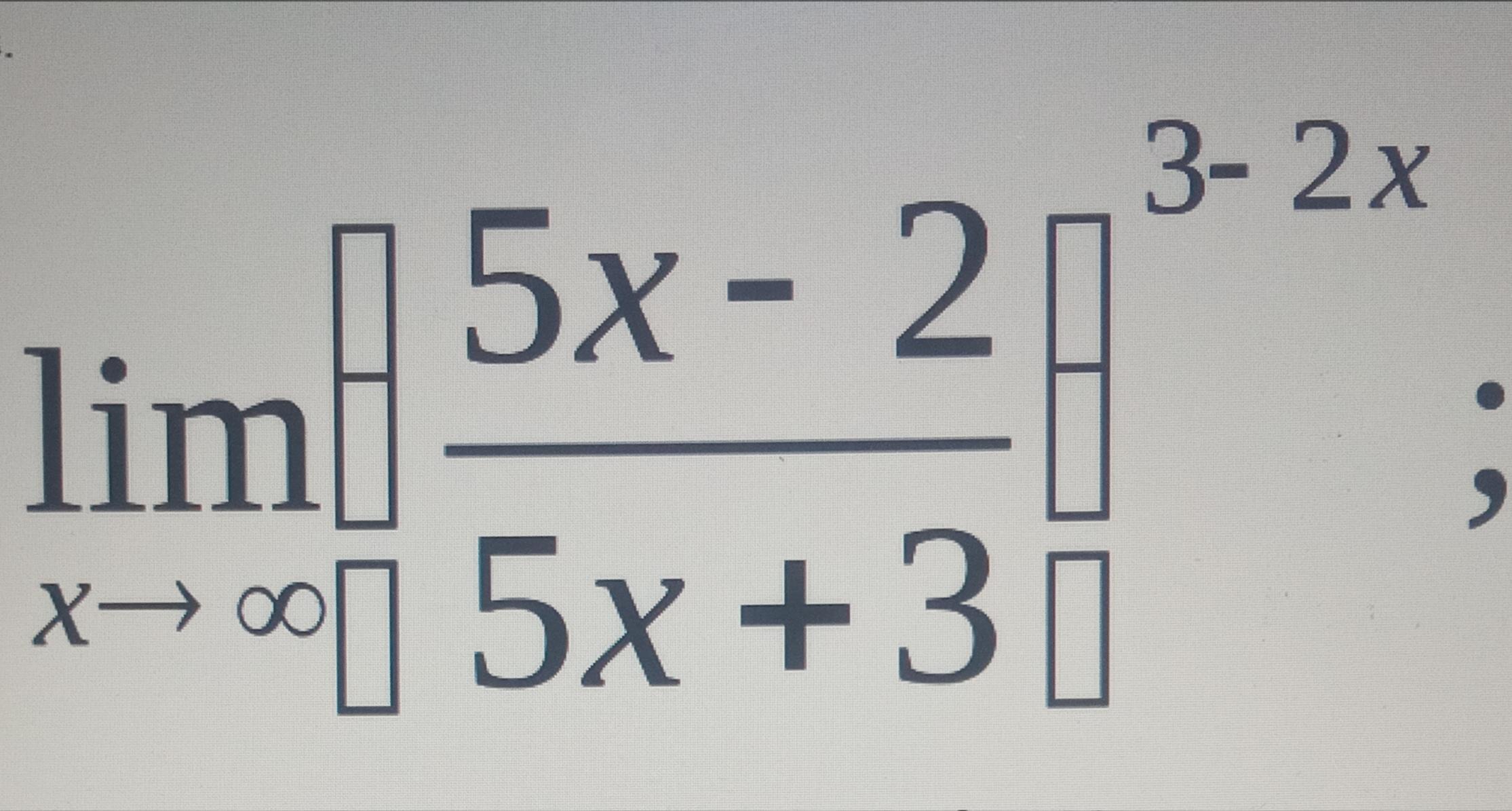
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Имеем дело с неопределенностью вида , обычно такие неопределенности сводят ко второму замечательному пределу.
Похожие вопросы
Предмет: Русский язык,
автор: gorohina
Предмет: Русский язык,
автор: elenavafina
Предмет: Английский язык,
автор: svetlajm12827
Предмет: Математика,
автор: KristinaKrivonosova
Предмет: Психология,
автор: saasha20041