Question

Из точки, на расстоянии 12 см от плоскости, проведены две наклонные, которые равны 37 см и 13 см. Найти проекции этих наклонных на плоскость.
Пожалуйста , дано, рисунок и полное объяснение решения​

Answer 1

Ответ: АН=35см; СН=5см

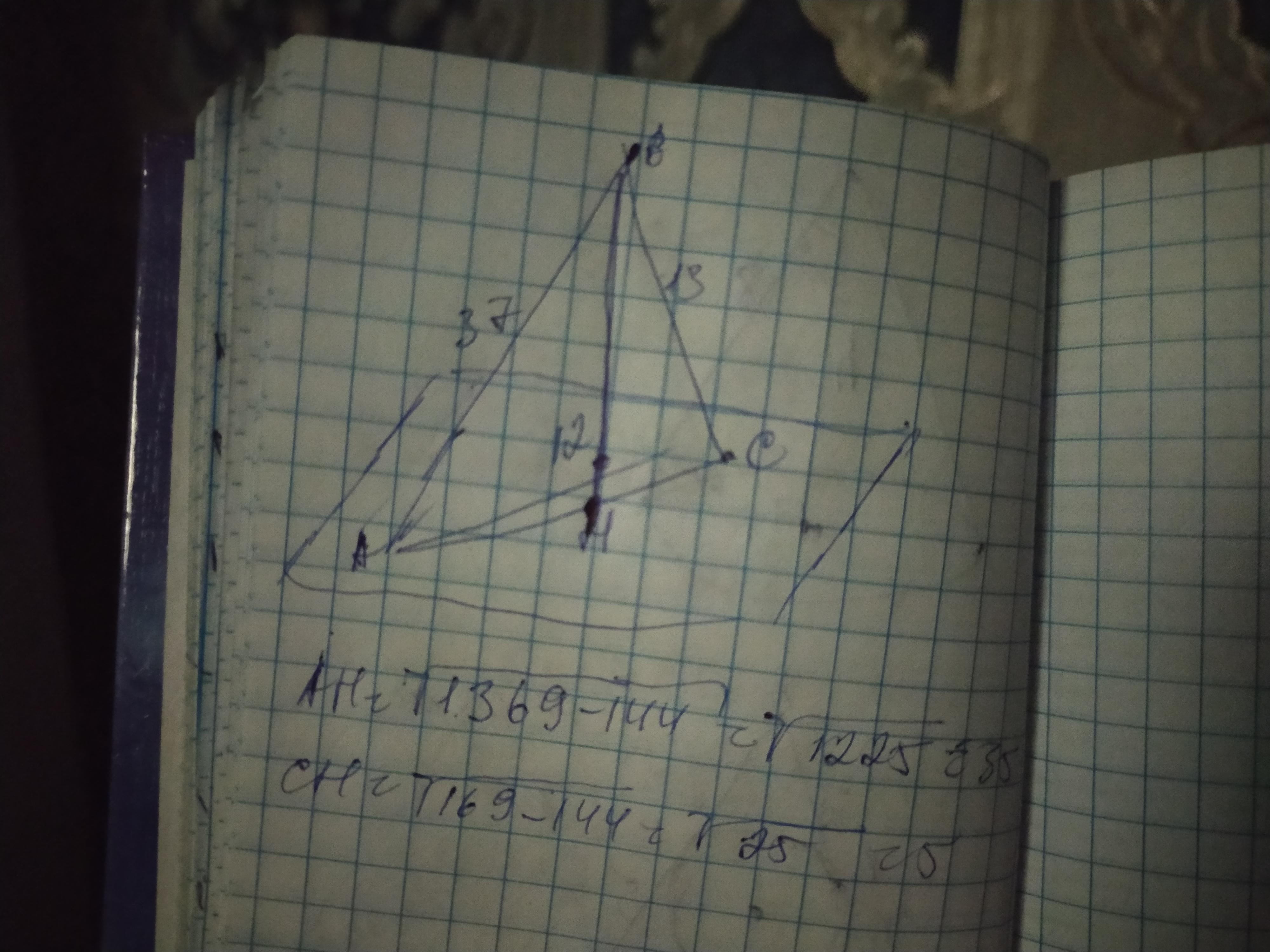
Объяснение: обозначим данные вершины А В С, а расстояние от точки до плоскости ВН. Так как расстоянием от точки к плоскости является перпендикуляр, то ВН перпендикулярно плоскости. У нас получился треугольник АВС с высотой ВН. ВН делит ∆АВС на 2 прямоугольных треугольника АВН и СВН, в которых наклонные АВ и ВС - гипотенуза, а ВН и АН и СН- катеты, причём АН и СН являются проэкция и на плоскость, найдём их по теореме Пифагора: АН²=АВ²-ВН²=37²-12²=

=1369-144=1225; АН=√1225=35см

СН ²=АВ²-ВН²=13²-12²=169-144=25;

СН=√25=5см