Предмет: Математика,
автор: Alisha6685
Исследовать функцию на монотонность и экстремумы с помощью производной y=1/3x³+3/2x²-4x+2
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Приложения:
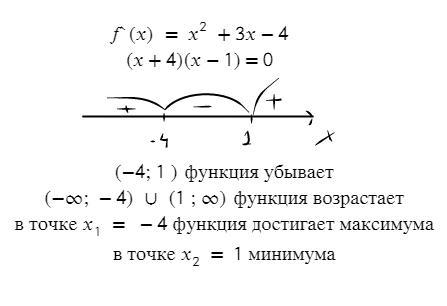
Автор ответа:
0
y'=((1/3)x³+(3/2)x²-4x+2)'=х²+3х-4
х²+3х-4≥0
По Виету корнями уравнения х²+3х-4=0 являются х=1 ; х=-4
Неравенство решим методом интервалов
____-4________1___________
+ - +
При х ∈[-4;1] функция убывает, при х∈(-∞;-4 ] и при х∈ [1;+∞) функция возрастает.
Точка х=-4-точка максимума ,максимум равен -64/3+24+16+2=62/3=20 2/3
Точка х=1- точка минимума, при переходе через нее производная меняет знак с минуса на плюс. минимум равен 1/3+3/2-4+2=-1/6
SergFlint:
Вы уже не первый раз пишете в отметках о нарушении, что в ответе нельзя использовать знак объединения. Откуда это? Не видел таких учебных пособий, где запрещено использовать знаки конъюнкции, дизъюнкции и т.д.
Похожие вопросы
Предмет: Русский язык,
автор: анягор
Предмет: Русский язык,
автор: lerkasemernina2014
Предмет: Русский язык,
автор: 07280066
Предмет: Математика,
автор: bubblewrap