Срочно 50 баллов 2 послед задания
Ответы
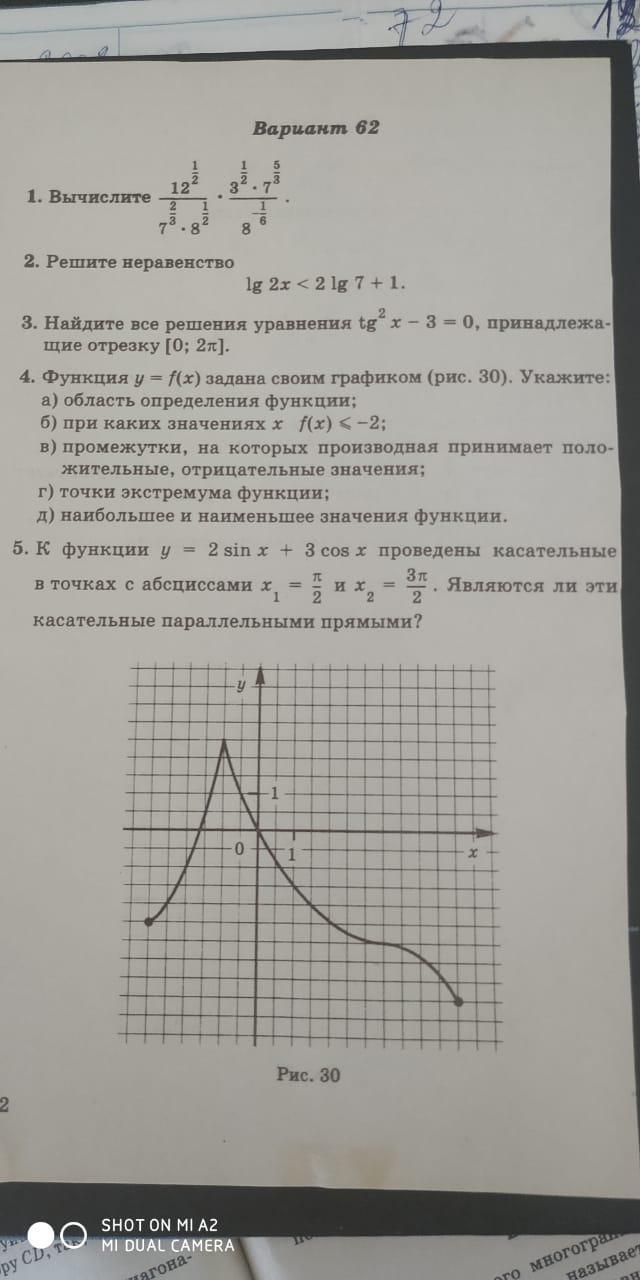
4. а) Область определения функции — это такие значения аргумента, при которых функция существует.
Из рисунка видно, что функция определена на
б) Следует определить, при каких значениях аргумента функция существует на
Из рисунка видно, что при
в) Производная принимает положительные значения, когда график функции
возрастает, и наоборот, производная
принимает отрицательные значения, когда график функции
убывает.
Таким образом, при
и
при
Здесь в точке производная равна нулю (из графика видно, что в этой точке происходит перегиб функции).
г) Точки экстремума — это такие точки на графике функции, при переходе через которые производная меняет свой знак на противоположный.
Производная при переходе через точку с абсциссой меняет знак с "+" на "–", значит имеем максимум в этой точке, и из графика
д) Из графика видно:
5. Уравнение касательной для функции в точке с абсциссой
имеет вид:
Для функции составим уравнения касательных в точках с абсциссами
и
Прямые вида будут параллельными, если их коэффициенты
будут одинаковыми.
В нашем случае и
, поэтому эти касательные параллельными не будут.
Ответ: нет, не являются параллельными прямыми.