Question

Определить четность-нечетность функции ()=3х^5+sinх+3

Answer 1

• функция чётная, если f(-x) = f(x), x ∈ $\mathbb{R}$;
• функция нечётная, если f(-x) = -f(x), x ∈ $\mathbb{R}$.

Определим четность-нечетность функции f(x) = 3х^5+sin(х)+3:

$f\left(-x\right) =3\left(-x\right)^5+\sin \left(-x\right)+3 = -3x^5 -\sin \left(x\right)+3\\-f\left(x\right) = -\left(3x^5+\sin \left(x\right)+3\right) = -3x^5-\sin \left(x\right)-3$

Проверяем функцию на четность:

$f\left(x\right)=3x^5+\sin \left(x\right)+3,\:f\spacef\left(-x\right)=-3x^5 -\sin \left(x\right)+3 \\f\left(x\right)\ne \:f\left(-x\right)$

$f(x)=3x^5+sin\:(x)+3$ — не является чётной функцией

Проверяем функцию на не четность:

$-f\left(x\right)=-3x^5-\sin \left(x\right)-3,\:f\spacef\left(-x\right)=-3x^5-\sin \left(x\right)+3\\-f\left(x\right)\ne \:f\left(-x\right)$

$f(x)=3x^5+sin\:(x)+3$ — не является нечетной функцией

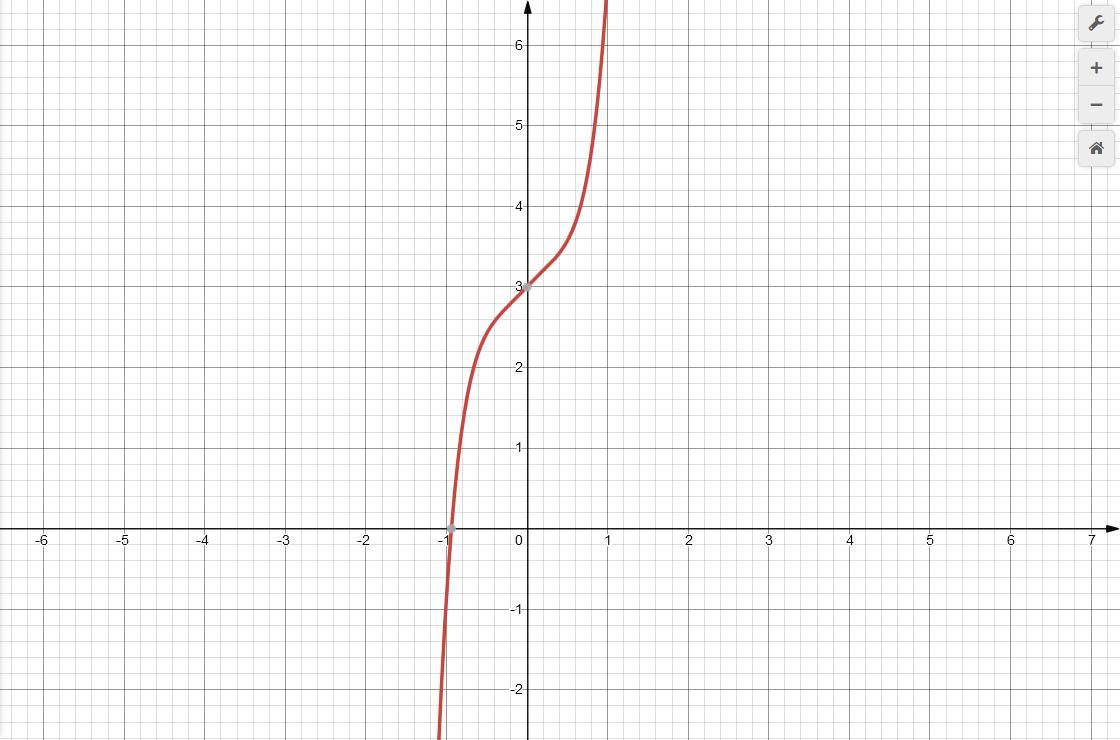
Ответ: f(x) = 3х^5+sinх+3 ни чётная, ни нечётная функция.