Question

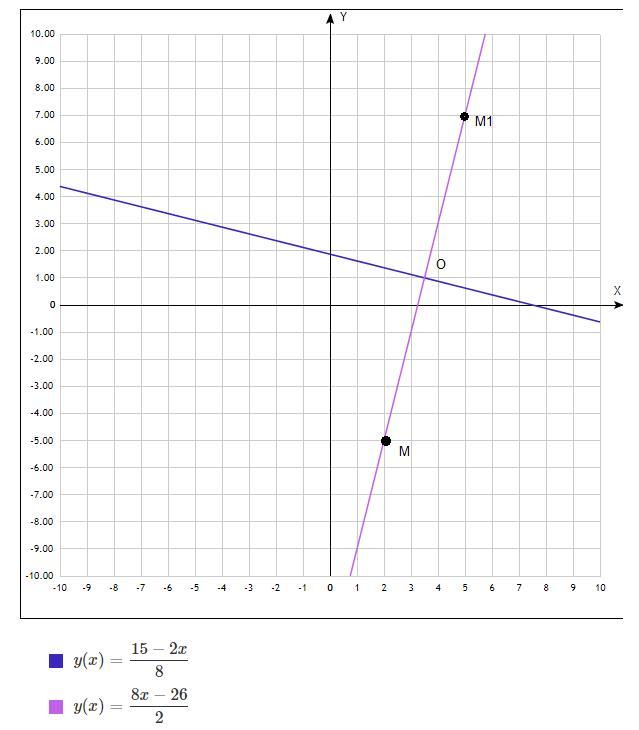
Определить координаты точки, симметричной точке M (2, −5) от- носительно прямой 2x + 8y − 15 = 0.

Answer 1

координаты симметричной точки лежат на прямой, перпендикулярной данной прямой и проходящей через точку М

тогда вид перпендикулярной прямой будет 8x-2y+c=0

(так как 2*8+8*(-2)=0-скалярное произведение их нормалей должно быть 0)

подставлю М

8*2-2*(-5)+c=0

c=-26

8x-2y-26=0-уравнение перпендикулярной прямой

теперь найду координаты точки пересечения О и отложу такое же расстояние от О в другую сторону

для этого решу систему

2x+8y-15=0  и 8x-2y-26=0

из второго y=4x-13 и в первое

2x+8(4x-13)-15=0

34x=119

x=3.5

тогда координата искомой точки  M1 по х равна 3.5+(3.5-2)=5

чтобы найти координату M1 по у . подставлю х=5 в уравнение y=4x-13

y=4*5-13=7

M1(5;7)