Найти площадь полной поверхности и объем правильной четырехугольной пирамиды, сторона основания которой равна 4 см, а высота 5 см. Буду благодарна за скорую помощь!!! :)
Ответы
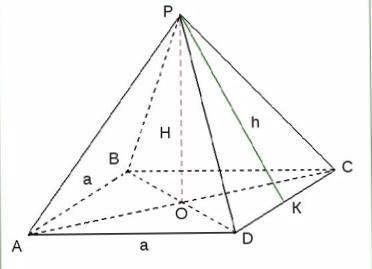
Дано:
Правильная четырёхугольная пирамида.
H = PO = 5 см
а = AD = 4 см
Найти:
S полной поверхности - ?
V - ?
Решение:
Так как данная пирамида - правильная, четырёхугольная => основание этой пирамиды - квадрат.
Квадрат - геометрическая фигура, у которой все стороны равны.
Квадрат - геометрическая фигура, у которой все стороны равны.=> AB = AD = CD = BC = 4 см
S квадрата = a², где a - сторона квадрата.
S квадрата = 4² = 16 см²
S боковой поверхности = 1/2Р * h, где P - периметр основания; h - апофема.
Апофема - высота боковой грани правильной пирамиды, проведённая из её вершины.
Проведём Апофема PK
Проведём прямую ОК.
РО = 5 см, по условию.
Так как ВС = 4 см => ОК = 4/2 = 2 см
Найдём РК, по теореме Пифагора: (c = √(a² + b²), где c - гипотенуза; a, b - катеты)
РК = √(PO² + PK²) = √(5² + 2²) = √29 см
Р = AB + AD + CD + BC = 4 * a = 4 * 4 = 16 см
S боковой поверхности = 16/2 * √29 = 8√29 см²
S полной поверхности = S основания + S боковой поверхности = 16 + 8√29 = 8(2 + √29) см²
V = 1/3а²H = 16/3 * 5 = 80/3 = 26 2/3 см^3
Ответ: 8(2 + √29) см²; 26 2/3 см^3.