Предмет: Алгебра,
автор: Lemah17
Помогите с решением , нужно найти производную функции
Приложения:
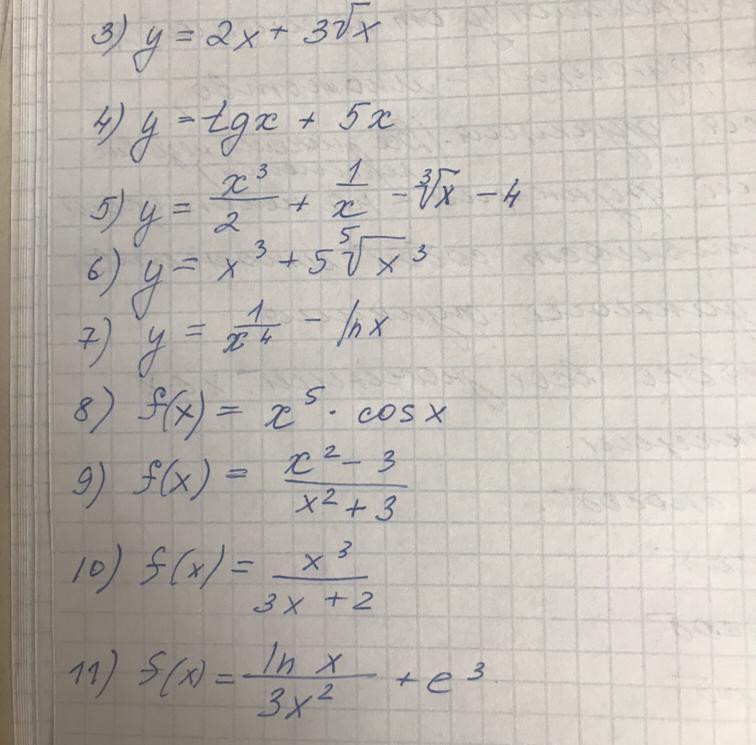
Ответы
Автор ответа:
1
Ответ:
Lemah17:
В 9-м примере в знаменателе степень так и остаётся?
да, она никуда не уйдёт...
В 10-м и 11-м не видно конечного ответа, обрезано
перезагрузите страницу, я за технические неполадки на сайте не отвечаю...
Похожие вопросы
Предмет: Английский язык,
автор: alenatishik
Предмет: Английский язык,
автор: frezer76
Предмет: Русский язык,
автор: татока
Предмет: История,
автор: Пельмешек12
Предмет: Математика,
автор: catxripunowa