Предмет: Алгебра,
автор: 8059
найти |a+b|, если a=25/a-b и b=144/b-a
Приложения:
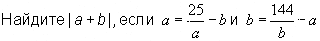
Ответы
Автор ответа:
0
так как модуль второе выражение так же равно 169/13=13
Похожие вопросы