help ! Найдите промежутки убывания функции
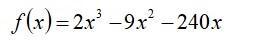
Ответы
производная равна 6х²-18х-240
Найдем критические точки.
6х²-18х-240=0
х²-3х-40=0
По Виету х=8; х=-5
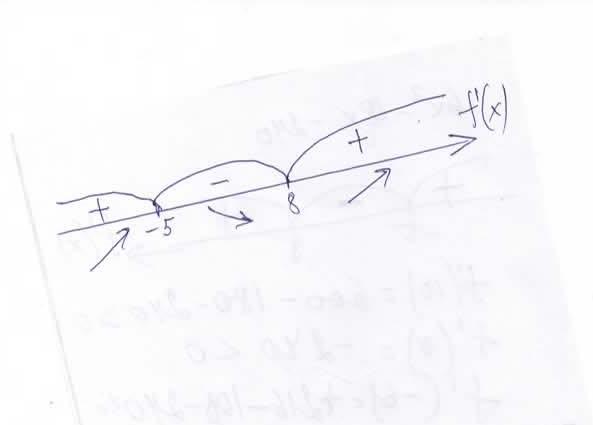
установим знаки производной на области определения функции
______-5________8_____________
+ - +
промежуток убывания [-5;8]
Ответ:f(x) возрастает на (-∞;-5) ∪ (8;+∞), f(x) убывает на (-5;8)
Объяснение:1)найдём ОДЗ: х∈R;
2) f'(x)= 6x²-18x-240
3) найдём критические точки, для чего приравняем производную к нулю: f'(x)=0, если 6x²-18x-240=0 ⇒x²-3x-40=0 ⇒ дискриминант D= 9+160=169=13² ⇒ x₁=(3+13)/2=8, x₂=(3-13)/2= -5, т.е. x₁=8, x₂= -5 - критические точки
4) Отметим критические точки на координатной прямой, они разбивают её на 3 интервала (выполнить рисунок): (-∞;-5), (-5;8), (8;+∞). Найдём знак производной в каждом из этих интервалов:
на (-∞;-5) f'(x)>0;
на (-5;8) f'(x)<0;
на (8;+∞) f(x)>0
если производная функции y=f(x) положительна для любого x из интервала (a;b), то функция возрастает на (a;b);
если производная функции y=f(x) отрицательна для любого x из интервала (a;b) , то функция убывает на (a;b) .
Значит f(x) возрастает на (-∞;-5) ∪ (8;+∞), f(x) убывает на (-5;8)