Question

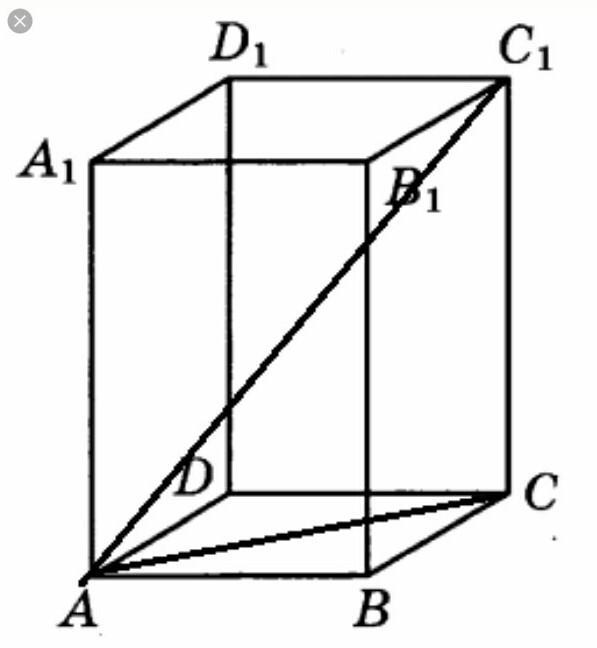
Диагональ правильной четырехугольной призмы равна l и образует с плоскостью основания угол. Определите площадь боковой поверхности призмы.

Answer 1

Ответ:

высота призмы h=LsinB

правильная, значит основания -квадраты, диагональ которых есть проекция диагонали призмы d=LcosB, a=d/√2=LcosB/√2, тогда Sбок=4*a*h=

4L²sinB*cosB/√2=2√2*L²sinB*cosB

Answer 2

Дано:

Правильная четырёхугольная призма.

АС1 = l

Диагональ АС1 образует с плоскостью основания угол.

Найти:

S боковой поверхности - ?

Решение:

Так как данная призма - четырёхугольная, правильная => основание данной призмы - квадрат.

"Квадрат - геометрическая фигура, у которой все стороны равны".

А все боковые грани - прямоугольники.

Угол между диагональю и плоскостью основания - угол между диагональю и её проекцией на плоскость основания.

Проекцией диагонали АС1 на плоскость основания - это диагональ BC квадрата ABCD => ∠С1АС - угол, образованный между диагональю АС1 и плоскостью основания ABCD.

Так как AC1 = I => AC = I * cos∠C1AC;

CC1 = h призмы = l * sin∠C1AC

Так как ABCD - квадрат => АС = АВ * √2 => AB = AC/√2 => AB = l * cos∠C1AC/√2 = I * √2 * cos∠C1AC/2.

S бок поверхности = Р * h, где Р - периметр основания; h - высота призмы.

Р = 4АВ = 2 * l * √2 * cos∠C1AC.

=> S бок поверхности = (2 * l * √2 * cos∠C1AC) * (l * sin∠C1AC) = 2√(2)l² * cos∠C1ACsin∠C1AC = sin(2∠C1AC) * √(2)l² = √(2)l² * sin(2∠C1AC) = l²√(2)sin(2∠C1AC)

Ответ: l²√(2)sin(2∠C1AC).